0 引言
電力系統負荷預測是電網能量管理系統的重要內容,通過精確的負荷預測,可以經濟合理地安排機組啟停,減少旋轉備用容量,合理安排檢修計劃,降低發電成本,提高經濟效益。常用的方法有非線性回歸、神經網絡法、時間序列法、模糊理論等。非線性回歸和時間序列法在電網情況正常、生產和氣象變化不大的時候預測效果良好,但不能考慮一些影響負荷的要素,如休息日、氣象等,當這些因素發生突變時預測精度受到影響。神經網絡和模糊理論考慮到了影響負荷的一些不確定因素,但沒有徹底解決網絡結構設計的難題,且需要較長的訓練時間。
SVM(支持向量機" title="支持向量機">支持向量機)是由Vapnik[1]最早提出的一種統計學習方法,近年來已經被成功地應用于語音識別、文字識別、時序數列預測等領域。研究顯示,該統計學習方法具有學習速度快、全局最優和推廣能力強的優點,其學習結果經常明顯好于其它的模式識別和回歸預測方法。本文將SVM理論應用于電力系統短期負荷預測" title="短期負荷預測">短期負荷預測,既考慮了影響負荷的諸因素,又建立了完善的數學模型。
SVM算法對與預測負荷曲線較平滑的系統,能夠取得較理想的效果。但是,對于慣性較小、隨機波動性較強的中小型電網,其效果相對較差。改進的方法是,先采用Fourier算法將歷史負荷曲線分解為平滑曲線和隨機波動曲線兩部分,只采用平滑部分作為SVM的歷史訓練數據,能夠取得更好的效果。
1 SVM線性回歸模型
假設有一組訓練數據,共有l個,其中第i個數據包含變量和與之相對應的變量xi∈Rn和與之相對應的變量yi∈R,SVM定義了一種機器(machine),用于確定x到y的映射關系x→f(X,a),a為可調參數,通過對已知數據的學習來確定它。在線性回歸中,定義映射函數f(x)=
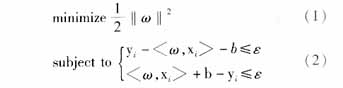
滿足(2)式有時候會使問題的求解變得非常困難,可以通過在目標函數中增加損失函數" title="損失函數">損失函數來進行處理,損失函數有多種形式,本文中只考慮ε-intensive損失函數:

式中C為常數,是回歸精度超過允許值的懲罰因子。(4)為有條件約束的優化問題,根據非線性規劃對偶性理論,對其建立沒有約束條件的Lagrange方程,并將最小值問題它轉化為對偶的最大值問題:
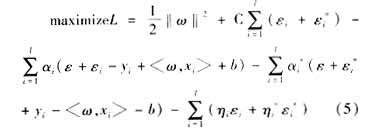
2 非線性回歸模型及其核函數" title="核函數">核函數
當然,現實中的大部分問題并不是簡單的線性問題,對非線性問題進行回歸,可以通過映射φ:X→τ把xi映射到特征空間τ,然后用核函數k(x,x′)=<φ(x),φ(x′)>來代替線性回歸中的
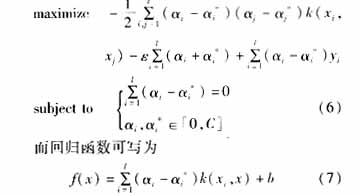
無論線性和非線性模型,都可采用內點法求解。
3 短期負荷預測的SVM與Fourier方法
3.1 樣本及其輸入輸出量的選擇
本文采用SVM方法來解決短期負荷預測問題。對于訓練樣本,首先通過聚類找出和預測點在星期屬性、節假日屬性、預測時段都相同的數據作為SVM中的y值,相應的x值(即樣本輸入量)分為如下幾類:
1)A={a1,a2,...,an} ,預測日之前n日內的在預測時段的負荷數據
2)B={b1,b2,...,bm},預測日前一日預測時段之前m個時段的負荷數據
3)C={c1,c2,...,cs},預測日的氣象預報,共s個數據,包含平均氣溫、最高氣溫、最低氣溫、風力、濕度等
4)D={d1,d2,...,dn} ,預測日之前日內的每日氣象數據,其中任何一個元素di包含s個如上所述的氣象數據
5)E={e1,e2,...,e7} ,預測日的周屬性,代表周一到周日,每個變量用1或0來表示
6)F ,一些從已知變量中通過某種計算演化而來的、對負荷的結果可能影響較大的數據(例如前一日溫度與該日預測溫度的差值、前二日與前一日在預測時段的負荷差值、該日前一周每天在預測時段的負荷平均值等)。
3.2 負荷預測的支持向量機模型
為了選擇合適的核函數,本文使用線性函數、多項式函數、徑向基函數、對數S型等多種核函數進行測試,發現徑向基函數的模型對于負荷預測問題精度最高,因此本文選用徑向基函數作為核函數。
假設按照上述樣本及其輸入輸出量的選擇構造的l個樣本集合為{(xi,yi),i=1,2,...,l},則負荷預測的支持向量機模型可寫為式(6)的形式,其中![]() 為徑向基函數。
為徑向基函數。
3.3 Fourier算法對歷史數據進行平滑處理
經數字實驗證明,上述短期負荷預測的SVM方法對于負荷慣性較大的大型電網有較理想的效果,但是,如果將它應用于具有較多沖擊性負荷(如軋鋼廠),其誤差較大。為了改進算法的預測效果,本文提出用Fourier算法對每日歷史負荷曲線進行Fourier變換,分解為平滑曲線和隨機波動曲線兩部分,只采用平滑部分作為歷史訓練數據,方法如下。
1) 對欲進行處理的一日負荷數據,檢驗其初始點負荷f(0)與終點負荷f(24)的差值是否小于給定的閾值δ。如果是, 說明該曲線基本滿足Fourier分解的基本條件f(0)=f(T);否則,進行時間軸的旋轉變換,使得f(0)=f(T);
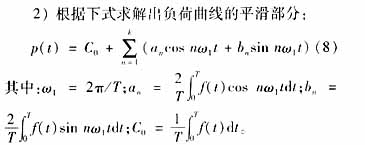
如果未經坐標軸變換,T取24(小時);否則,取坐標變換后的時間軸對應初始負荷點與終點的坐標差值。
k的取值視電網負荷曲線的波動情況而定。取值應越大,擬合效果越好,但是其濾波作用越差。經過數字實驗發現,k取15對波動性較大的地區性電網能有較理想的濾波效果且與原曲線擬合較好。
3) 如果經過了坐標軸變換,將數據再還原到原始時間坐標軸。
4 計算結果與誤差
本文采用的算例是根據由常州電力公司提供的2003年3月1日至4月24日的每天氣溫數據和每天288點的負荷數據,預測4月25日全天96點的數據。為了考察本文所使用的方法的精度,還采用BP神經網絡法和SVM算法(無Fourier分解)進行了預測。圖1到圖3分別示出三種方法的該日的預測情況。
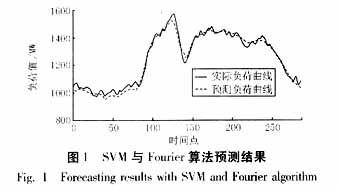
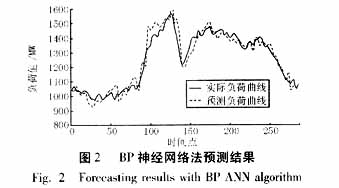

本文所提出的算法計算的該日的最大相對誤差(絕對值)為5.2%,平均誤差為2.4%。對比神經網絡法(平均誤差4.1%,最大相對誤差11.9%)和單純SVM算法(平均誤差3.7%,最大誤差10.1%)的誤差結果,該法具有較高的精度。本文所提算法對每個點進行預測,訓練程序運行時間都在400毫秒到1500毫秒之間(含濾波時間),測試時間則小于20毫秒,具有較快的速度。
5 結論
本文介紹了SVM和Fourier算法及其在電力系統短期負荷預測中的應用。算法考慮到影響負荷的要素,對歷史數據聚類,找出與預測點屬同一類的數據進行訓練。Fourier算法將負荷曲線平滑化,防止了隨機波動對預測的干擾。算例證明,該方法結果合理,運行速度快,精度很高,是一種很有應用價值的新興算法。

