電梯群控系統(EGCS)采用優化的控制策略來協調多臺電梯的運行，以提高電梯的運輸效率和服務質量。
　　由于電梯群控系統控制目標的多樣性，同時也由于電梯系統本身所固有的隨機性和非線性，僅僅通過傳統的控制方法很難提高控制系統的性能。近年來智能控制得到迅速發展，其方法在解決具有此類特點的系統上有獨到之處。自從Mistubishi公司首次把模糊邏輯用于電梯系統，采用模糊控制的電梯群控系統數量迅速增加。例如用模糊逼近的方法來確定群控系統呼梯分配中的重要參數——區域權重，進而得出評價函數的值，實現系統多目標控制^[1]；利用專家系統來實現電梯群控系統的模糊控制^[2]等。但這些方法的判斷標準均有不足之處，只考慮了某一類因素，并未考慮到乘客的平均等待時間、能源消耗等因素；同時在做模糊邏輯推理時沒有把時間量、進/出人流量等作為輸入變量。本文提出了新的最優評價函數，綜合考慮乘客的平均等候時間(AWT)、長時等待率(LWP)、能源消耗(RNC)三個主要標準，并根據實際要求給予不同的權重，以此來合理分配電梯。AWT、LWP、RNC三個量可由一定的模糊規則推理而來，通過運用從經驗豐富的電梯工程師獲得的各種控制規則，比僅僅用嚴格的補償函數方法，可以獲得更好的效果。但由于單純的模糊控制缺乏學習功能，存在系統性能受知識的影響、調整確定隸屬函數需大量的仿真實驗、規則修改不便等缺點。而人工神經網絡通過調整連接權來得到近似最優的輸入輸出映射，因此適用于建立類似電梯群控系統的一類非線性動態系統。兩者結合的模糊神經網絡(FNN)，具有一個表達框架，一方面提供用于解釋和推理的可理解的模型結構，另一方面具有知識獲取和學習能力。本文把AWT、LWP、RNC的規則映射到神經網絡中，利用網絡的學習功能來調整改善規則，解決了隨機性、非線性等問題。
1 目標函數的選擇
　　對于多個電梯的群控系統，所選的控制策略是，每部電梯處理各自的隨機指令，而對于層站召喚信號則由調度算法進行分配。調度算法實際上是一個評價函數。評價函數的確定主要用到以下三個評價標準：
　　· 平均等候時間(AWT)：所有乘客的候梯時間和乘梯時間的平均量；
　　· 長時等待率(LWP)：在一定時間內等待時間超過60s的乘客占總乘客數的百分比；
　　· 運行量(RNC)：在一定時間內電梯的運行次數。由于能源消耗由啟/停電梯決定，所以該標準可決定能源消耗的大小。
　　
　　其中：S_i——評價函數，表示第i個電梯響應某個層站信號的可信度。i＝1...n，n表示群控系統的電梯數。
　　三個評價標準可由一定的模糊規則推理得到。由(1)式可求出各電梯的可信度S₁、S₂、...S_n。由下面的(2)式可求出最適合響應層站召喚信號的電梯m，它對應著最大的S_i。
　　
　　在(1)式中W的不同選擇表明了對三個評價標準的不同側重。例如在上/下班高峰，選擇電梯時以減小乘客等待時間為主要考慮因素而節約能源為輔，故LWP所對應的權重大一些；而在晚上乘客稀少，則以節約能源為主，故RNC所對應權重可大一些，而LWP所對應的權重則小一些。
2 規則的知識表示及推理
2.1 模糊規則的知識表示
　　在電梯群控系統中運用從經驗豐富的電梯工程師獲得的各種控制規則，比僅僅用嚴格的補償函數方法，可獲得更好的效果，它可很好地處理系統中的多樣性、隨機性和非線性。
　　層站召喚分配部分把新的層站召喚信號分配給合適的電梯，在分配時要考慮召喚方向和所在樓層、電梯狀態以及未來層站召喚等信息。AWT_i、LWP_i和RNC_i的模糊估計需用到HCWT_i、maxHCWT_i、CV_i和GDi，分別定義如下：
　　HCWT_i—層站召喚信號從產生到被第i個電梯響應的等待時間。
　　maxHCWT_i—分配給第i個電梯的所有層站召喚信號的最大HCWTi。
　　CV_i—第i個電梯響應未來層站召喚信號的能力，與乘客的進出電梯流量有關。
　　GD_i—新的層站召喚信號的產生位置與被第i個電梯響應的所有召喚信號(包括層站召喚和梯內召喚)產生位置之間的最短距離。
　　CV_i說明如下：
　　
　　其中的in_person表示在將來單位時間內試圖進入電梯i的乘客，fail_person表示在單位時間內層站召喚信號沒被響應的乘客。可看出CV_i越大，響應將來層站召喚信號的能力越強。
　　HCWT_i越小，說明層站召喚信號被響應的時間越短，則乘客的候梯時間小。但因電梯i的啟/停頻度增加，梯內乘客的乘梯時間相應地變長，結果所有乘客的平均等待時間AWT_i一般會增加。
　　我們把文獻中的共性知識和具有豐富實踐經驗的電梯專家的個性知識加以總結，仔細推敲，歸納了如表1的AWT_i、LWP_i和RNC_i模糊規則，用IF－THEN語句來表示。其中輸入變量均為模糊化后的值。

　　變量的隸屬度函數取為高斯型，隸屬度函數的中心值a、寬度b要根據實際需要適當調整，以滿足減小AWT、LWP、RNC的多項要求。
2.2模糊神經網絡的知識存貯及推理
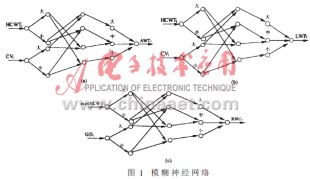
　　根據前面的模糊規則表，可把這些模糊規則映射到模糊神經網絡(FNN)中，從而提高推理的智能性。該網絡提供了解釋和推理的可理解的模型結構，通過它可以以一種清晰的方式描述知識，模糊規則可用網絡的節點對象、連接權對象、連接結構等來翻譯解釋；同時具有知識獲取和學習能力。與上述規則表相對應的模糊神經網絡分別如圖1(a)、(b)、(c)所示。

　　由于該網可通過知識的表達和學習，記憶交通信息，然后用推理方式推出AWT、LWP、RNC三個量，所以是一種智能推理。考慮到輸入參數的模糊化和輸出參數的去模糊化，該模型總共有5層。其中第1層為輸入層，輸入參量為標準化后的量，在(0，1)之間；第2層為模糊化層，對輸入值分別模糊化為大、中、小三種語言變量；第三層是規則層，其神經元個數由專家知識確定的規則個數決定，該層與第2層的連接完成模糊規則前提條件的匹配，實現“模糊邏輯與”的運算；第4層為結論節點層，將具有相同結論又被激活的規則節點的輸出放在一起實現“求和”運算，得到輸出隸屬度函數值；第5層為輸出層完成去模糊化。各層節點的輸入函數和輸出函數可選取如下：
　　

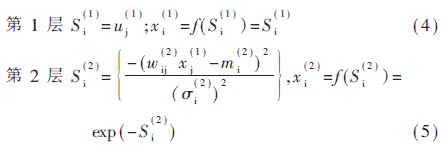
　　其中S、X 分別表示輸入、輸出函數，W為權值，Ni表示第i層的節點數。根據(4)～(8)式及網絡結構圖即可分別推理出第i個電梯的AWT、LWP和RNC，并帶入(1)式求得第i個電梯響應層站召喚信號的可信度，(1)式中W的選擇根據交通模式的不同給予不同的權重。以此類推，分別求出其它電梯響應該信號的可信度，并根據(2)式求出最大可信度從而選擇最合適的電梯調度。
3 規則的改善
3.1 中心值與寬度的修改
　　網絡中各節點及所有參數均有明顯的物理意義，其初值可根據模糊規則來確定。鑒于電梯群控系統的復雜性和一些因素的不確定性，可通過網絡的學習不斷修改和完善規則，提高調度的準確性。學習一般采用BP算法，如每層的權值均作修改，可以稱為全部層學習，其缺點是計算量大。對于模糊規則，中心值、寬度應選擇恰當以滿足減小AWT、LWP、RNC的要求。針對模糊神經網絡的隸屬度函數，給出了中心值、寬度學習算法。修正的學習參數采用了動量項方法，它實際上相當于阻尼項，有利于減小學習過程的振蕩，改善收斂性^[3]。對于圖1的模糊神經網絡，第二層為模糊化層，輸入隸屬度函數有中心值、寬度兩個參數，它們是模糊化的關鍵。在學習樣本已知的情況下，可只對網絡的中心值、寬度進行學習，同樣可減少學習時間和計算量。其算法如下：

　　
　　i＝1…N2，N2為第2層的節點個數，N3為第3層的節點個數；δ_pi⁽²⁾為在第p個樣本下反傳到第2層的誤差；x_pi⁽²⁾為在第p個樣本下第2層第i個節點(神經元)的輸出函數；s_pi⁽²⁾為在第p個樣本下第2層第i個節點的輸入函數；m_pi⁽²⁾為第2層第i個節點的隸屬度函數中心值；σ_pi⁽²⁾為第2層第i個節點的隸屬度函數寬度。
　　(2)寬度修改的推導同前，有：
　　
3.2 部分層修改
　　對于FNN，某一層的權值根據實際物理意義可能為一確定值，即使交通信息的訓練樣本變化也不希望對該層權值進行修正，若啟動全部層學習將使該層權值改變，失去了實際的物理意義，并有可能使學習不收劍，發生振蕩。為此利用部分層學習，此算法可根據實際的需要對網絡的某一層或某幾層進行學習。仍采用誤差反傳的原則，當前饋到某一層時，如該層需要學習，則對該層的權值進行修改。否則，不需要修改，但該層的誤差需通過網絡的內部連接傳到上一層。該算法可節省學習時間，減少計算量。對圖1的網絡，一般第四層的權值是學習的主要參數，為此可只對該層權值進行學習。修正該層權值的目的是改善交通規則間的相對重要性，使重要規則的作用得以加強，提高電梯調度的智能性。
3.3電梯的調度
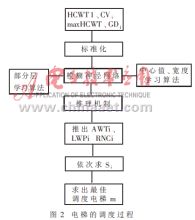
　　根據以上介紹，總結電梯調度過程如圖2，此種電梯調度方法很好的解決了層站召喚信號的隨機性、不確定性給電梯調度所帶來的問題。而隸屬度函數和規則的修改使神經網絡模型能適應變化著的交通狀況，有利于提高調度的智能性。

4 仿真結果
　　根據以上的交通模式判別策略和調度算法，我們用VB編制了電梯仿真軟件系統^[4][5][6]，該系統具有電梯參數設置、仿真、性能統計、交通模式判別、系統幫助等功能。考慮到系統的開放性、可擴充性、柔性等特點，采用了面向對象的分析和設計方法。在群控系統中每個電梯均可看成一個對象，對象之間通過消息進行通訊。采用本文所介紹的調度策略進行了仿真實驗，仿真條件如圖3，仿真比較結果如圖4。結果表明AWT、LWP性能均提高，而RNC性能則降低。這是因為在此仿真時段對能源消耗的重要性要求降低所致，反映在仿真條件上是RNC對應的權重相比其它兩項較小。

?

參考文獻
1 Chang Bum Kim, Kyoung A.seong, etc, ″A fuzzy approach to elevator group control system″,IEEE Trans Syst., Man, Cybern.,1995；25(b):985～990
2 Seiji, etc, ″Supervisory control for elevator group by using fuzzy expert system″, Proceedings of the IEEE International Conference on Industrial Technology, Guangzhou, 1994
3 孫增忻等，智能控制理論和應用，南寧：廣西科學技術出版社，1996
4 Edward Yourdon&Carl Argila, Case studies in object oriented analysis & design, Publishing house of elec－tronics industry, 1998.6
5 Ronald J.Norman, Objected－oriented systems analysis and design, Prentice－hall international, inc., 1998.6
6 彭克松等譯，電梯交通分析與控制，北京：中國建筑科學研究院機械化研究所，1993