??? 摘 要:在動態場景中,碰撞檢測遇到的最明顯的問題就是需要對N個物體對進行兩兩求交測試,其時間復雜度達到O(N2)。提出了一種簡化球體的BSP剖分結構的快速碰撞檢測算法。首先用一種調度算法估計BSP樹開始失衡的地方,再用一種策略來選擇分割面,新結構在表示動態場景中不需要重新構建樹,而是在保持樹的平衡和合理的高度的同時通過自身的調節來達到更新。
??? 關鍵詞:碰撞檢測;動態場景;BSP樹
?
??? 在動態場景的模擬中,當場景中物體的個數超過2個,碰撞檢測遇到的最明顯的問題就是需要對所有N個物體進行兩兩求交檢測,其時間復雜度達到O(N2)。為此,加快這種檢測速度通常是用兩步算法[1]。所謂兩步法,就是在第一步(也稱初步檢測階段),首先將多數明顯不相交的物體對進行快速排除,找出潛在的相交區域或潛在的相交物體對;然后在第二階段根據已經確定的潛在的相交區域或潛在的相交物體對幾何做進一步的相交測試,這一步也稱詳細檢測階段。在處理動態場景初步檢測時,BSP樹算法在快速排除明顯不發生碰撞的物體不夠理想,為此本文提出了一種基于BSP結構的快速碰撞檢測算法。該算法是在BSP樹結構的更新操作時,定義了5種操作算子,并通過一種調度策略執行算子,保持BSP樹結構的平衡。
1 BSP樹的構建
??? BSP樹是最常用的空間剖分技術,Fuchs 于1980 年首次將BSP技術中剖分平面的定側性質應用于多邊形場景的剖分[2],BSP 樹是一個用來對 n維空間內多面體進行排序和查找操作的標準的二叉樹。這個樹代表了整個場景,每一個葉節點代表著場景的1個凸集多邊形集合,每一個非葉節點包含一個分割平面,這個分割平面將1個子場景分成2個更小的場景。BSP 樹的構造是這樣一個過程,已有一個子場景,用這個場景中1個多邊形所在的平面從內部分割這個場景,結果又得到2個子場景然后繼續循環分割它們,直到所有子場景都是一個凸集多邊形集合為止。BSP樹就是一個二叉樹,葉節點存儲場景多邊形,非葉節點存儲分割面。圖1所示,為二維平面上的BSP樹結構剖分。
?
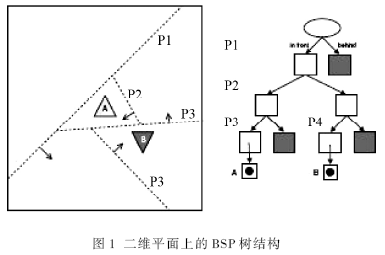
??? BSP在計算碰撞檢測時有巨大的優勢,它能夠很容易定位運動物體在BSP樹的具體位置,即場景中的具體位置。定位完成后,只有很少數目的多邊形需要檢測,即每一幀里只檢測物體是否穿過那些組成它所在葉節點的多邊形[3-4]。
2 簡化球體BSP剖分結構的分割面選取策略
??? 當創建一個 BSP 樹時,決定是否需要一個平衡樹,也就是說樹的左右分支的深度的差異不應該太大,由于每一次分割都會產生新的多邊形,因此應盡量減少分割的次數。如果在 BSP 樹的創建過程中產生了太多的新多邊形,顯示卡就要花更多的時間來處理多邊形的渲染,使一個不平衡的樹將用更長的時間來進行樹的遍歷。因此在選擇分割面時,應該根據下面的標準(p為分割面) :
??? population(p)由分割面所生成節點所包含物體的數目。
??? balance(p)被分割面分割成的左右子樹深度的比率。
??? redundancy(p)橫跨分割面的物體的數目。
??? 即在選擇分割面時,需要綜合考慮以上3個條件,選擇balance最大、redundancy最少的分割面。
????分割面的選取方法一般采用直接選擇平面法,是指從表示場景的多邊形集合中隨機選出一個多邊形,假定該多邊形在空間范圍內無限延展,則平面將空間分成了2個子空間。在各自2個子空間內,原有的場景多邊形分別位于其中,對于某一子空間,再從其中的多邊形集合中任意選取1個,作為該子空間的超平面。這一過程遞歸進行,直到最終的子空間中只有唯一的景物為止。圖2給出了這一過程的圖形示意。
?
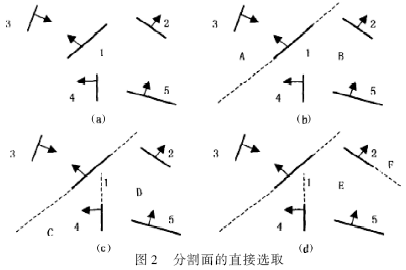
??? 圖2中,把各線段看作是垂直于紙面的平面,箭頭為該平面的法向量,箭頭所指方向為該平面的前面(可見一側),其相反方向即為該平面的后面(不可見一側)。圖2(a)給出了初始的場景多邊形集合以及每個多邊形的法向量,在圖2(b)中,首先選取面1為分割面,將空間分為A, B兩個子空間;在B子空間中選取面4為分割面,將B分為C, D兩個子空間;在D子空間中選取面2為分割面,將D分為E、F兩個子空間。至此,整個空間劃分完畢,每個子空間中只含有一個景物。
3 簡化球體BSP剖分結構的更新操作
??? 由于要保持動態物體在動態場景中的高效率的運動和一定的搜索特性,導致了BSP樹結構的改變。如果重新構造樹,額外的開銷將嚴重影響碰撞檢測的效率,因此,希望在原來樹的基礎上通過局部更新得到新的樹。在這種情況下,更新樹的過程時間開銷就相當重要,如果更新樹所花費的時間和完全重建差不多,更新就沒有什么意義了。更新操作必須能夠實時完成。本文采用的方法是根據動態物體的物理位置把它插入到BSP樹的相應節點下,用BSP樹邏輯操作修改BSP樹的結構。下面將介紹是如何被調度來執行更新的。
3.1 分裂操作算子
??? 當葉節點包含物體數量(population)大于給定的葉節點包含物體數量的閾值時,將該節點向下分裂,如圖3所示。這樣,一個新的分割面產生1個節點,同時生成兩個左右子樹。對于產生內部節點的分割面的選取按照上一部分提到的分割面的選擇方法。對物體在候選分割面法線上的投影進行分類支配著這個操作的開銷,為了減少這種開銷只考慮這些物體1個子集。
?

?
3.2 移除分裂操作算子
??? 這個操作通過用存儲在BSP樹中的葉結點的信息來降低因分類而導致的使用分裂操作的開銷。
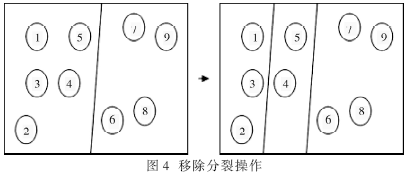
??? 在BSP樹的構造過程中,每個葉節點將被整個放入表中。也就是從根節點(內節點)開始在節點上沿著它的父分割面的法線放置物體。在這張表中可以找出另一個法線方向與父分割面法線方向相平行的分割面。如果這個新的分割面滿足分割面選擇標準,就可以用移除分裂操作來代替分裂操作,如圖4所示。
?
?
3.3 合并操作算子
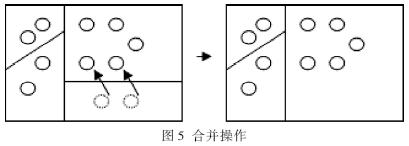
??? 合并操作算子的作用是:當一個葉節點連同它的兄弟所含物體數量之和還沒超過閾值時,將它們向上合并。而且當由于物體的運動使分割面分割的區域出現空值時,它負責重新移動此分割面,(如圖5)。
?
?
??? 所有存儲在合并節點的子樹的葉節點的物體的有序表需要合并成一個。左右子樹的節點自下而上合并,并且葉子節點代替原來的節點,如圖6所示。每一個表需要沿著新的方向分類。當合并節點包含物體數量很少時,合并節點的子樹通常也很小。
?

?
3.4 平衡操作算子
??? 平衡操作算子的作用是:在原來樹的基礎上通過最小的改變來修復開始變得不平衡的節點。它適合于左右子樹的深度差異很大的節點,即1個節點的1個子樹所含物體數量很多而另一個子樹幾乎是空的。在這種情況下,利用平衡操作來取代合并子樹操作,并通過移動分割面重新建立平衡,如圖7所示。如果這個移動的分割面滿足選擇分割面的標準,可利用平衡操作來修改這個節點。
?

?
3.5 交換操作算子
??? 交換操作算子的作用是:它適合于當平衡操作失敗于重新建立平衡時的情況,在合并操作之前使用交換操作。交換操作刪除不平衡的節點,用包含物體數量多的子樹的根節點代替刪除的不平衡節點結構的調整所需要的只是將包含物體數量少的子樹插入,但這個操作很快,因為這個子樹幾乎是空的,如圖8所示。
?

?
4 簡化球體BSP剖分結構更新操作調度策略
??? BSP樹結構的更新不同于物體位置的更新,因為樹結構更新的時間開銷很大,而且結構更新的好壞會導致碰撞檢測對數目的增減,如果結構更新失敗就會導致碰撞檢測對數目的增加。定義的更新是在規定時間間隔內達到一個折中,即在更新的時間開銷和樹的高度之間。結構操作執行的時間順序是至關重要的。更新BSP樹結構的結構操作的調度策略說明如下:。
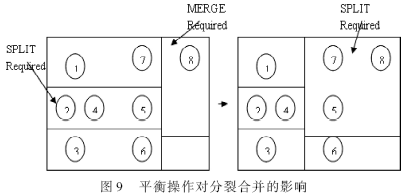
??? 平衡操作是通過調整分割面來改善平衡,但是它會產生改變物體分布的副作用。這可能影響其他操作,在某些情況下可能變得不必要了。因此,在其他操作之前應該先考慮平衡操作,如圖9所示。
?
?
??? 分裂操作是非常關鍵的,因為它是要把1個大的存放物體信息的順序表分成2個小表,以降低更新順序表的代價。首先是集中在所包含物體數量小于閾值的葉節點上,也就是通過對場景中的物體數量動態調整葉節點。而移動分裂操作是在分裂操作之前執行,也就是只有當移動分裂操作失效時才開始執行分裂操作。
??? 當平衡操作失效時,交換操作開始執行。這個操作也如同平衡操作一樣會產生副作用,通常導致小數量的物體移動。
??? 合并操作是消除包含物體數量小于閾值的葉節點。這個操作不是很重要,因為對于小的順序表的維持是很快的,而且額外的開銷是保持幾乎是空的節點和最小限度的葉節點。只有當在模擬的更新周期期間有自由的時間,這個操作才會被執行。
??? 更新BSP樹結構的結構操作調度策略如下:
??? 開始遍歷根節點為N的BSP樹:
??? (1) If 節點N是不平衡節點;
????(2) then評估平衡操作算子;
??? (3) If 平衡算子有效執行平衡操作;
??? (4) Else 調用交換算子;
??? (5) 停止遍歷;
??? (6) End if ;
??? (7) 檢查移動分裂操作,分裂操作,合并操作和調度時間表;
??? (8) if 所有事件已調度,停止遍歷;
??? (9) Else 重復執行1~8步遍歷節點N的每個子樹;
??? (10) End if;
??? (11) 根據調度時間表估算被執行的事件數目;
??? (12) 執行移動分裂操作;
??? (13) 執行分裂操作;
??? (14) 執行交換分裂操作;
??? (15) 執行合并分裂操作。
5 實驗結果與分析
??? 為了驗證BSP算法的性能,與QT quad(tree),Spatial Hash(SH)、LO loose(octrees),SP sweep-and-(prune)這4種算法進行了一系列比較實驗。所有的實驗都是在PIV2.5GHz、512MB內存的PC機上進行的。
??? 每個模擬實驗按每秒25步被評估4 min。實驗評估包括執行效率(FPS),碰撞檢測對的數目,初步碰撞檢測階段的時間,更新的時間(物體位置的更新時間和數據結構的更新時間)。
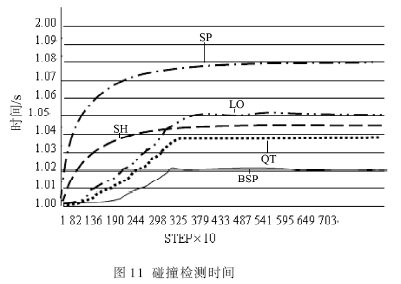
??? 實驗物體落入有限制的區域中,然后跟區域中的其他物體相互碰撞,這是利用了動態和靜態物體之間的空間分割方法。因為靜態物體對于提高執行速度是至關重要的。這種情景最適合BSP。BSP的碰撞檢測時間最少,QT次之。SP的碰撞檢測時間最壞但是更新時間跟BSP差不多。LO更新時間最佳。SH的更新時間最壞。
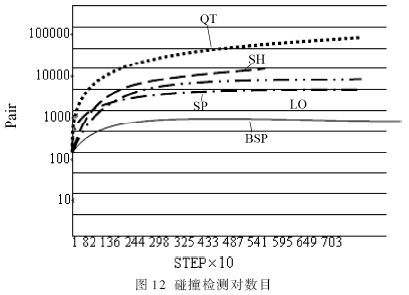
??? 實驗測試結果分別如 圖10、圖11、圖12、圖13所示。
?

?
?
?

?
??? 本文所介紹的方法主要目的是當碰撞檢測對數目增加時,在計算碰撞檢測對的代價和在空間數據結構中的結構更新代價兩者之間建立一個折中的方法。實驗結果表明,在初步碰撞檢測階段與SH、SP和LO方法相比,本文的方法是很有效的。雖然在碰撞檢測對數目上與QT相似,但與QT相比,文中的方法對靜態物體導致的空間分割模擬或者是高度集中的環境中產生太多碰撞的模擬是比較好的。文中各個更新BSP樹結構的結構操作和調度策略的設計可以更好地重新利用存儲在樹中的信息來重新定位分裂面和穩定的執行效率。初步碰撞檢測只是這種方法的一個應用,用這種方法來加快其他幾何體的碰撞是今后要研究的另一個方面。
參考文獻
[1] HUBBARD P M. 1995. Collision detection for interactive graphics applications. IEEE Transactions on Visualization and Computer Graphics, 1995, 1(3): 124-133.
[2] ?FUCHS H, KEDEM Z M,NAYLOR B F. H1 On visible surface generation by a priori tree structure [J]. Computer Graphics ,1980 , 14 (3) : 124-133.
[3]?AR S, MONTAG G, TAL A. Deferred, self-organizing BSP trees. Computer Graphics Forum, 2002, 21(3): 269-278.
[4]?JAMES D L, PAI D K. BD-Tree: Output-sensitive collision detection for reduced deformable models. ACM Transactions on Graphics (SIGGRAPH), 2004, 23(3).

