摘? 要: 綜述了對Rijndael算法所提出的各種攻擊并對其進行分析。同時對一些可能會導致對Rijndael攻擊的新理論和研究結果做了分析和討論。
關鍵詞: Rijndael? 攻擊方法? 安全性分析
?
2000年10月,美國國家標準技術研究所(NIST)宣布Rijndael被確定為高級加密標準(AES)。本文給出目前攻擊Rijndael密碼的一些主要方法。
關于Rijndael的完整密碼的系統規范本文并沒有詳細描述,讀者可以參考文獻[6]。本文僅對Rijndael算法所提出的攻擊作一個整體的概述。另外還介紹了目前已經公布的可能可以破解Rijndael密碼的思想。表1中總結了對于給定密鑰長度所能攻破的方法的復雜性、攻擊的輪數。在表1中已經公布的能攻破Rijndael密碼的輪數都小于Rijndael密碼的規定的輪數。例如,在2000年公布的基于不可能差分分析(impossible differential)的攻擊方法只能對于6輪的128位密鑰進行攻擊,而其標準是10輪。
表1中,幾乎所有的攻擊(除了在2001年公布的攻擊方法外)都是在NIST將其作為AES標準之前就已經公布了。因此可以得到結論:到目前為止,對于Rijndael密碼的攻擊還沒有比窮盡密鑰搜索攻擊更有效的方法,已經公布的攻擊思想不能形成有效的攻擊。

?
對于Rijndael密碼更詳細的攻擊的討論的一些新思想將在下文中詳細討論。在后一部分列舉和簡單討論了目前已知的對Rijndael密碼的攻擊方法,在第3部分對最近提出來的攻擊Rijndael密碼的新思想(代數攻擊)進行討論。
1? 對Rijndael密碼的攻擊
1.1 差分和線性分析
差分和線性分析方法是到目前為止二種最有用的通用密碼分析方法。對于這些攻擊提供輪數低的復雜度是在設計Rijndael密碼時的最基本的準則。
對于Rijndael密碼來說,已經證明對于一個4輪的Rijndael密碼來說,差分分析方法的概率上限是2-150,線性分析方法的概率上限是2-75。結合實際Rijndael密碼的輪數,這些輪數對于抵抗上述攻擊能夠提供足夠的安全性。對于這方面更詳細的討論可以參考文獻[6]。
1.2 變量法
在變量法公布之后,線性和差分攻擊方法在某些方面已經做了擴展,也公布了一些和它相關的攻擊方法。最好的擴展方法是截段差分分析法(truncated differentials)。但是在設計Rijndael密碼的時候就已經考慮到這種攻擊方法,Rijndael密碼能夠比較好地抵抗這種攻擊。其他的攻擊方法還有:
不可能差分攻擊:差分密碼攻擊是利用高概率特征或差分恢復密鑰,不可能差分攻擊是利用概率為0(或非常小)的特征或差分,其基本思想是排除那些導致概率為0(或非常小)的特征或差分的候選密鑰。對5輪的Rijndael密碼,可以用不可能差分攻擊方法,它要求229.5個選擇明文、231個密文、242個存儲字和226小時的預先處理時間,該結果在參考文獻[4]中做了改進,使得它可以攻擊6輪的Rijndael密碼。但是對于輪數更高的Rijndael密碼,采用該方法攻擊則沒有更好的效果。
Square攻擊:對Rijndael密碼分析最有效的就是Square攻擊,它是一個選擇明文攻擊,通過研究基于字節結構的密文來進行攻擊。它對于和Rijndael密碼的其中一輪有相似結構的任何密文都是有效的。這種攻擊的其他名字還有“飽和攻擊”(Lucks在參考文獻[11]中提出,這種攻擊能夠破解具有7輪的192位和256位Rijndael密碼),L.Knudsen和D.Wagner提出的“積分密碼分析”,以及A.Biryukov和A.Shamir提出的“結構攻擊”。
最初的Square攻擊對6~7輪的Rijndael密碼(例如AES-128和AES-192)的破解比窮盡密鑰搜索攻擊快。N.Ferguson等在減少破解的工作方面做了一些優化,因此,它能夠在有256位相關密碼的277個明文,2224個密文,破解9輪的AES-256密碼。
Collision攻擊:這種攻擊是由Gilbert和Minier提出[9],它對于破解7輪的AES-128、AES-192、AES-256仍然是最好的破解方法。
2? 一些新的理論和分析
盡管前面介紹了能夠對簡化的Rijndael密碼的攻擊方法,但是這些方法對Rijndael密碼本身的攻擊并沒有任何效果。上述的大多數攻擊方法都和稱為“代數攻擊”的方法有關,可以簡要地歸納為如下步驟:
(1)收集信息階段:密碼分析者將密文表達為有很多變量的一系列簡單方程。這些變量包括明文、密文和密鑰中的位或字節,還有一些中間計算結果和輪密鑰。
(2)攻擊階段:密碼分析者利用輸入的數據,例如明文—密文對等,代替在第一步中得到的方程中的變量,并且用各種辦法將方程解出來,這樣就可以根據求出的變量來恢復密鑰。
按照Rijndael密碼的設計原則,Rijndael密碼是用一些比較巧妙的方程表達式來實現的。雖然從單純的數學角度來看,要從這些方程組表達式得到密碼的密鑰非常困難,但是也可能利用其他的一些方法比較容易地解決。已經有一些方法利用Rijndael密碼的代數結構來破解密碼。但是到目前為止還沒有能夠進行有效攻擊的方法,大多數文章的結論還有待于進一步研究和探討。下面討論在這方面最新的一些研究成果和理論。
(1)連分式。Ferguson,Schroeppel和Whiting[8]得出一個關于Rijndael密碼的閉公式,該公式可以看作是由一個連分式生成的。在5輪以后中間結果的任何字節都可以表示為如下表達式:
????
在上述表達式中,每個K是一個字節,它依賴于擴充了的密碼中的一些字節;每個Ci是一個已知的常數;每個*是一個給定的指數或下標。但是這些值依賴于它們所包含符號的求和變量。一個完全擴展的式(1)的版本有225項。為了破解一個10輪的Rijndael密碼(AES-128),密碼分析者可以通過二個這種類型的方程來利用計算的中間結果。第一個方程可以將5輪以后的中間變量作為明文字節函數;第二方程可以將6~10輪以后的中間變量作為明文字節函數。結合二個方程可以得到一個含有226個未知變量的方程。通過重復這個方程226/16個給定的明文/密文對,從信息理論的意義上來說,就有足夠多的信息能夠解出未知變量。但是到目前為止,還沒有任何人公開發表能夠具體地去尋找一種算法來解決這樣一類問題的方程。
(2)XSL。Courtois and Pieprzyck[5]通過研究發現,在Rijndael密碼中使用的S-盒可以通過一系列隱含的二次布爾方程表達。用字母x1,……x8表示輸入的位,用字母y1,……y8表示輸出的位。則存在如下形式的等式:
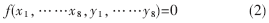
其中函數f為二次方程。
從理論上來說,只需要8個像(2)式的方程就能夠定義S-盒,但是Courtois and Pieprzyck經研究發現,能夠構建多于所需要的方程個數。此外,他們還宣稱這些特定的方程可以有助于簡化解決問題的復雜性。他們發現一個算法,該算法在處理這個問題的時間復雜度低于指數。可是有很多的研究者懷疑他們計算的正確性。例如Don Coppersmith曾說過“我堅信Courtois-Pieprzyk的工作是有漏洞的。他們把線性獨立的方程個數估計過多了,他們所得到的結果事實上沒有足夠的線性方程來解決問題”。此外,他還說“這種方法有一定的優點,也值得去研究,但是并不能像他們所說的那樣能夠破解Rijndael密碼。”T.Moh也懷疑他們計算方法的正確性。無論如何,在假設他們的計算方法正確的前提下,破解密碼的復雜性的最好估計是2255步(對于不同參數的復雜性的計算可以參見文獻[5]的8.1節)。這就意味著,他們的攻擊僅僅可以破解Rijndael密碼為256位的密鑰(AES-256)。因為相應的窮盡密鑰搜索攻擊的復雜度為2256。現在還不清楚Rijndael密碼的什么屬性影響到該攻擊的復雜性。這種攻擊方法對AES的影響不會太大,因為即使這種攻擊方法完全正確,AES的安全性也比DES好得多。
(3)嵌入法。Murphy and Robshaw[12]定義了分組密碼BES,它是對128字節為一組而不是128位為一組的對象來處理。按照Murphy and Robshaw的觀點,BES密碼的代數結構甚至比Rijndael密碼的代數結構更簡單。此外,Rijndael密碼能夠被嵌入BES密碼中,也就是說有如下映射φ:

在這個方程中,K代表密鑰,x代表明文。Murphy and Robshaw通過研究得出BES的一些性質。但是BES的屬性不能轉換為Rijndael密碼的性質。
Murphy and Robshaw相信,如果將XSL方法應用到BES,則解決步驟的復雜性將比直接將XSL方法應用到Rijndael密碼的復雜性大大降低。
(4)雙密文攻擊。在文獻[1]中介紹了雙密文的概念,它基本是“嵌入”技術的歸納。其基本內容為:如果取三個不可逆映射f,g和h,則存在一個雙密文DUAL滿足:
????
在這個方程中,K代表密文密鑰,x代表明文。這個方程表示對于一個給定的明文和密鑰雙密文產生相同的密文文本。從這個意義上來說,雙密文等價于原來的密文。因此,可以實現和分析雙密文而不是原來的密文。在文獻[1]中確定了Rijndael密碼中的240個雙密文。到現在,還沒有關于雙密文有何漏洞的報導。一個類似的概念,稱為Rijndael-GF[6]。已經證明,對于抵抗差分和線性密碼分析,Rijndael-GF族密碼系統的密文都具有相同的安全性。
(5)Plaintext-dependent Repetition Codes攻擊。2003年1月8號,Eric Filiol發表了一篇文章[3],在該文中他宣稱可以用一種非常簡單、快速和惟密文的攻擊方法來攻擊AES。其基本思想是:假設pi,ci和ki分別為AES的明文、密文和密鑰位。這些位的變化范圍總是0~127,0是第一個字節的最重要的位,127是最后一個字節最不重要的一個位。例如c71是密文中第9個字節的最重要的位。在文章中,作者宣稱如果明文是以形式:

?
以大概是0.50003的概率成立。如果該論斷能成立,則該方法對AES的攻擊大約只須231步即可。目前,這種論斷還沒有取得一致的認可,有些密碼分析者懷疑其正確性。
3? 結束語
在本文中,主要展示和討論了到目前為止,所有關于Rijndael密碼系統的密碼分析成果。此外還討論了有可能能夠破解Rijndael密碼的一些新的可能的攻擊方法。但是有些方法還有待于進行進一步的證明和探討。
?
參考文獻
1? Barkan E,Biham E.In how many ways can you write?Rijndael?In:Proceedings of Asiacrypt′02,Queenstown,
New Zealand,2002
2? 馮登國.密碼分析學.北京:清華大學出版社,2000
3? 楊義先,孫偉,鈕心.現代密碼新理論.北京:科學出版社,2002
4? Cheon J H,Kim M J,Kim K et al.Improved Impossible Differential Cryptanalysis of Rijndael and Cryp? ton,Information Security and Cryptology-ICISC 2001,2001
5? Courtois N T,Pieprzyk J.Cryptanalysis of block?ciphers with overdefined systems of equations.In:
Proceedings of Asiacrypt′02,Queenstown,New Zealand,2002
6? Daemen J,Rijmen V.The Design of Rijndael.Information Security and Cryptography,Springer Verlag,2002
7? Ferguson N,Kelsey J,Lucks S et al.Improved cryptanalysis of Rijndael.In:Proceedings of Fast Software
Encryption-FSE′00,New York,NY,USA,April,2000
8? Ferguson N,Schroeppel R,Whiting D.A simple algebraic representation of Rijndael.In:Proceedings of
Selected Areas in Cryptography-SAC′01,Toronto,Ontario,Canada,August,2001
9? Gilbert H,Minier M.Acollision attack on seven rounds of Rijndael.In:Proceedings of the Third Advanced
Encryption Standard Conference,New York,USA, April,2000
10? Knudsen L R,Wagner D.Integral cryptanalysis(extended abstract).In:Proceedings of Fast Software
Encryption-FSE′02,Leuven,Belgium,February,2002
11? Lucks S.Attacking seven rounds of Rijndael under 192-bit and 256-bit keys.In:Proceedings of the
Third Advanced Encryption Standard Conference,New York,USA,April,2000
12? Murphy S,Robshaw M J B.Essential algebraic structure within the AES.In:Proceedings of Crypto′02,
Santa Barbara,California,USA,2002

