摘 要： 簡要分析了徑向基函數(shù)(RBF)神經(jīng)網(wǎng)絡。在此基礎上，介紹了K-均值聚類算法的神經(jīng)網(wǎng)絡、C-均值聚類算法的神經(jīng)網(wǎng)絡和PAM聚類算法的神經(jīng)網(wǎng)絡三種聚類算法的RBF神經(jīng)網(wǎng)絡。展望了基于聚類的RBF神經(jīng)網(wǎng)絡設計的發(fā)展趨勢。
關鍵詞： 聚類； RBF神經(jīng)網(wǎng)絡； 發(fā)展趨勢
徑向基函數(shù)(RBF)神經(jīng)網(wǎng)絡是前向型神經(jīng)網(wǎng)絡[1]，能夠以任意精度逼近于任意函數(shù)。因為RBF網(wǎng)絡結構相對簡單、非線性逼近能力強和收斂速度較快，現(xiàn)在已經(jīng)廣泛應用在工業(yè)智能控制和系統(tǒng)優(yōu)化、通信系統(tǒng)的信號以及信息處理等諸多領域。對該網(wǎng)絡的深入研究也越來越受到國內(nèi)外學者的共同關注。而聚類分析[2-3]是一種對數(shù)據(jù)進行分析和建模的重要方法，即將沒有明顯規(guī)律的數(shù)據(jù)源，依據(jù)某些特性，將數(shù)據(jù)劃分到有區(qū)別的數(shù)據(jù)類中，所采用的聚類算法就是聚類分析研究的重點。本文綜述了三種聚類算法是如何構造RBF神經(jīng)網(wǎng)絡。
1 RBF神經(jīng)網(wǎng)絡結構及其原理
RBF神經(jīng)網(wǎng)絡的原理[4]是模擬人腦中局部協(xié)調(diào)和相互覆蓋接收范圍的神經(jīng)網(wǎng)絡構造。它是一種三層前向網(wǎng)絡，由輸入量到輸出量的映射存在非線性，而隱含層空間到輸出空間的映射卻是線性的，從而提高了學習速度，同時也避免了局部極小問題。RBF神經(jīng)網(wǎng)絡結構如圖1所示。它具有n個輸入節(jié)點、m個隱含節(jié)點和1個輸出節(jié)點。
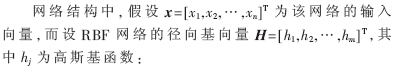
構造和訓練RBF神經(jīng)網(wǎng)絡就是要使它經(jīng)過學習來確定每個隱層神經(jīng)元基函數(shù)的中心和寬度，然后再利用最小二乘或其他方法求出隱含層到輸出層的權值向量，從而構建出所研究系統(tǒng)的輸入到輸出的映射關系。
2 聚類的RBF神經(jīng)網(wǎng)絡設計
對RBF神經(jīng)網(wǎng)絡來說,隱層節(jié)點中心和基函數(shù)寬度的初始值的確定會直接影響神經(jīng)網(wǎng)絡的收斂速度,因此選擇合適的兩個參數(shù)的初始值可以提高收斂速度,其選擇方法有很多，比如有梯度下降法、模糊理論算法和自適應模糊等方法。而本文就是綜述K-均值聚類算法、C-均值聚類算法和PAM聚類算法,利用不同的聚類分析算法得到隱層節(jié)點中心和基函數(shù)寬度,從而構造和訓練出合適的RBF神經(jīng)網(wǎng)絡。
計算過程從一個隨機的聚類中心開始，通過尋找目標函數(shù)的最小點，反復調(diào)整聚類中心和各個樣本的隸屬度，在Jc的局部最小點處收斂，最終達到確定樣本類別。
近，即d(Pj,Ph)≥d(Pj,Pj2)，則Pj2是Pj的第二最近中心點。此時若將Ph替換Pi作為中心點，則Pj∈Pj2所代表的組，因此就Pj來說替換的代價為Cjih=d(Pj,Pj2)-d(Pj,Pi)；
3 發(fā)展趨勢
要進一步提高聚類算法對RBF神經(jīng)網(wǎng)絡隱層節(jié)點中心和基函數(shù)寬度的確定，需要優(yōu)化改進現(xiàn)有的聚類算法，以提高學習性能。因此，出現(xiàn)了一些在原聚類算法基礎上改進的聚類算法[8-10]，彌補了樣本分析在聚類過程中存在的某些不足,將聚類算法的性能發(fā)揮得更加充分，能更有效地與RBF神經(jīng)網(wǎng)絡結合起來。
參考文獻
[1] 蘇美娟.徑向基函數(shù)神經(jīng)網(wǎng)絡學習算法研究[D].蘇州:蘇州大學，2007.
[2] CHIU S L. Fuzzy model identification based on cluster estimation[J]. Journal of Intelligent and Fuzzy System，1994，2(3)：1240-1245.
[3] 滿春濤，李曉霞，張禮勇.一種基于ACO的RBF神經(jīng)網(wǎng)絡訓練方法[J].哈爾濱理工大學學報，2008，13(1):59-61,65.
[4] 劉金琨.先進PID控制及其MATLAB仿真[M].北京:電子工業(yè)出版社，2003.
[5] 吳曉蓉.K-均值聚類算法初始中心選取相關問題的研究[D].湖南:湖南大學，2008.
[6] 何迎生，段明秀.基于模糊聚類的RBF分類器的設計與實現(xiàn)[J].重慶科技學院報，2009，12(2):101-103.
[7] 段明秀，孫可.基于PAM聚類方法的RBF神經(jīng)網(wǎng)絡設計[J].沈陽師范大學學報,2009，27(4):440-443.
[8] 朱長江，張纓.模糊Ｃ-均值聚類算法的改進研究[J]. 河南大學學報，2012，42(1):92-95.
[9] 李春富，鄭小青，葛銘.基于改進聚類算法的RBF網(wǎng)絡及其應用[J].南京工業(yè)大學學報，2011，33(6):72-76.
[10] 龐振,徐蔚鴻.一種基于改進K-means的RBF神經(jīng)網(wǎng)絡學習方法[J].(2011-07-14).[2012-01-20]：http://www.cnki.net/kcms/detail/11.2127.TP.20110714.1550.036.html.