文獻標識碼: A
文章編號: 0258-7998(2010)10-0132-04
1980年4月Anderson第一次闡述了入侵檢測的概念,指出可以使用審計網絡數據的方式判斷非法入侵的發生[1]。在網絡數據的審計中,沒有一種確定的函數關系可以鑒別非法入侵。因此引入機器學習的方法,作為入侵行為和網絡數據特征之間模型進行函數逼近。
機器學習的方法在入侵檢測領域應用廣泛,并有較好的檢測效果。傳統的機器學習算法需要大量的網絡數據,而正常的網絡數據特征有著小樣本、高維數、多變性的特點。支持向量機(SVM)對小樣本、高維數的數據有著較好的訓練能力,已經被應用于入侵檢測[2]。最小二乘向量機(LSSVM)是SVM中的一種,相比SVM有著更快的運行速度。LSSVM懲罰因子C和核函數參數?滓的選擇使用網格搜索,耗時且分類精度不高。而粒子群優化(PSO)算法的尋優求解能力較為突出,可以利用PSO算法對LSSVM的相應參數進行選擇[3]。
PSO算法中一個重要的參數就是慣性權重w。w較大時,全局搜索能力較強;w較小時,局部搜索能力較強。基本PSO算法采用固定w,搜索的性能和效率不高。參考文獻[4]提出了讓w隨著進化的進行而線性減少的策略,相應的PSO算法稱為線性權重下降PSO(LWDPSO)算法。該PSO算法在提高搜索效率的同時有著早熟收斂、陷于局部最優的缺點。本文提出一種改進的PSO算法,即并行PSO算法。該算法將粒子群分成兩組[5]進行協同搜索,兩組粒子具有不同的w,其中w較大的粒子組側重全局搜索;w較小的粒子組側重在w大的粒子組找到全局最優位置的附近區域進行精細搜索。每組都有一部分固定的粒子,其余的粒子根據進化階段動態分配給兩組,通過動態分配粒子保證算法初期以全局搜索為主,后期以局部搜索為主。通過適應度函數的仿真實驗,證明了并行PSO算法的尋優性能更優。

選用RBF函數作為核函數:
2 PSO算法
PSO算法源于對鳥類覓食行為的模擬,通過鳥群之間的集體協作使群體達到最優。標準PSO算法初始化產生一群粒子,每個粒子以一定的速度在n維空間里飛行,飛行速度由個體的飛行經歷和群體的飛行經歷動態調整。X1=(Xi1,Xi2,…,Xin)是粒子i當前的位置,V1=(Vi1,Vi2,…,Vin)是粒子當前的速度,P1=(Pi1,Pi2,…,Pin)是粒子i所經歷過的最好位置,在這個位置粒子i擁有最佳適應度。設f(x)為最小化的目標函數,則粒子i的最好位置由下
3 改進PSO算法
粒子群進化前期應該以全局搜索為主,搜索整個空間,但不能放棄局部搜索,因為全局搜索的粒子速度較快,發現的位置的范圍雖然廣泛,但精度不高,容易錯過全局最優位置;進化后期應該以局部搜索為主,但不能放棄全局搜索,因為局部搜索雖然精細,但搜索的范圍較小,無法搜索到較遠的更優位置。
本文提出一種改進PSO算法,即并行PSO算法。設粒子的數量為S,總進化代數為G,當前進化代數為i。該算法將粒子群分成兩組,運行PSO算法時慣性權重w分別設置為0.95和0.4,其中w為0.95的粒子組側重全局搜索,w為0.4的粒子組側重在w為0.95的粒子組找到全局最優位置的區域進行精細搜索。每組粒子都有一定基本的粒子數量,均為S/4。剩余S/2粒子根據進化階段動態分配給兩組,分配給w為0.95的粒子組為S×(G-i)/2G(朝負無窮方向取整);分配給w為0.4的粒子組為S×i)/2G(朝正無窮方向取整)。
進化初始,w為0.95的粒子組粒子數目最多,達到3S/4,進行全局搜索,余下的S/4 w為0.4的粒子組對全局搜索到的當前最優位置的小范圍區域進行局部搜索,期望在該區域中搜索到更優位置;進化后期,動態粒子逐漸從w為0.95的粒子組調整到w為0.4的粒子組,空間已被w為0.95的粒子組多次搜索,w為0.4的粒子組針對當前最優位置的相關小范圍區域進行局部搜索,w為0.95的粒子組在對空間中當前全局最優位置的相關大范圍區域進行搜索,不放棄任何尋找到全局最優位置的機會。
4 仿真實驗及分析
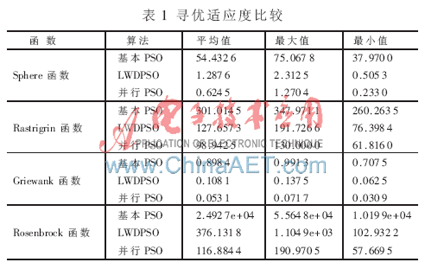
使用四種典型的測試函數[6]: Sphere函數、 Rastrigrin函數、Rosenbrock函數和Griewank函數作為適應度函數進行測試。各算法最大進化代數為500代,種群規模為80,優化方程的維數為30,c1、c2等于2,搜索的空間為[-100,100]。為避免實驗中偶然性現象,現將PSO三種算法針對這四種函數同時進行了10次實驗。圖1~圖4分別是四種測試函數對三種算法的適應度變化與進化代數比較曲線圖。表1是三種算法在10次實驗次數中取得的適應度的平均值、最大值和最小值。


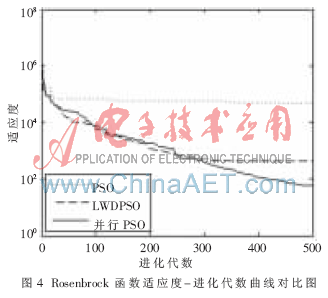
基本PSO算法粒子一直進行全局搜索,沒有進行局部精細搜索,因此無法找到較優位置,適應度值一直較大,尋優效果較差;LWDPSO算法在前期有較好的搜索效果,但是在中后期收斂之后對最優位置的搜索沒有任何突破,早熟的跡象非常明顯;并行PSO算法有著較好的全局搜索能力以及局部收斂能力,對最優位置的搜索較為穩定,避免了局部最優,沒有早熟的缺點,同時搜索到了最優位置。同時從表1可以得出:基本PSO算法的尋優較差,得到的適應度遠遠高于其他兩種算法;LWDPSO算法的尋優結果優于基本PSO算法,次于并行PSO算法;并行PSO算法的尋優結果優于基本PSO算法和LWDPSO算法,實驗得到的適應度平均值、最大值和最小值在三種算法中都是最低的。
5 基于并行PSO算法的LSSVM建模方法
將LSSVM的懲罰因子C和δ核參數映射成粒子,根據并行PSO算法進行優化選擇,最終使得建立的模型估計值與期望值的逼近程度達到預期目標。其算法流程如下:
(1) 并行PSO算法參數初始化,將粒子群分成兩組,慣性權重w分別設置為0.95和0.4。
(2) 根據設定的適應度函數,計算每個粒子的位置。
(3) 將粒子的位置與自身最優位置進行比較,如果當前位置相應適應度小,則更新自身最優位置。
(4)比較每個粒子的自身最優位置適應度求出全局最優位置。
(5) 根據當前進化代數動態調整兩組粒子的數目,進行下一代進化。
(6) 所有進化次數結束,將此時全局最優粒子分別映射為懲罰因子C和核參數?滓,并以此為優化結果,建立模型。
6 實驗過程及結果
6.1實驗數據預處理
實驗中采用的數據取自1999年DARPA為KDD競賽提供的一個異常檢測的標準數據集,它是由美國麻省理工學院的Liconln實驗室通過模擬一個典型的美國空軍網絡而獲得原始的TCP/IP網絡通信數據,對于每一個TCP/IP連接,提取了41個屬性。數據中有四種類型的攻擊:未經授權的遠程訪問(R2L)、拒絕服務攻擊(DoS)、對本地超級用戶的非法訪問(U2R)和掃描與探測(Probing)。標識為正常的數據占19.6%,攻擊數據占80.4%。
實驗中的訓練數據取自于原始數據集中kddcup數據,測試數據取自于corrected數據,訓練數據和測試數據采用等間隔的選取方式。測試數據共選取54 220條,其中正常數據12 140條、攻擊數據42 080條,訓練數據共33 520條,按類型和間隔平均分成10組,分別使用10組訓練數據建立模型對測試數據進行測試,實驗結果取10次實驗的平均值。
實驗中,需要對數據進行處理,實驗數據的protocol-type、sevice和flag屬性使用字符串表示,對其進行數字替換處理,對屬性中不同的類型使用不同的數字表示。另外,必須要對所有屬性進行歸一化處理,公式為:

其中new為歸一化后的數據,old為歸一化前數據,max為屬性的最大值,min為屬性的最小值。
6.2 實驗結果
網格搜索、LWDPSO算法和并行PSO算法分別對LSSVM的參數尋優,并建立各自的模型,對測試數據集進行了檢測。實驗結果如表2所示。

從表2可以得出,由于訓練數據和測試數據采自不同的數據集,網格搜索和LWDPSO算法的檢測率較低,誤報率和漏報率較高;采用并行PSO算法對LSSVM進行參數尋優所建立的入侵檢測模型檢測率、誤報率和漏報率都優于其他兩種算法參數尋優后所建立的模型。
本文給出并分析了基本PSO算法和LWDPSO算法的定義及特點。提出并行PSO算法,將粒子群分成兩組,分別設置不同的慣性權重,慣性權重大的粒子組側重全局搜索,慣性權重小的粒子組側重在慣性權重大的粒子組找到全局最優位置的附近區域進行精細搜索。根據進化代數動態調整兩組中進化的粒子數,并給出了每組粒子的數量調整公式。通過四個適應度函數仿真實驗,證明了并行PSO算法的尋優性能優于基本PSO算法與LWDPSO算法。通過入侵檢測實驗測試,并行PSO算法對LSSVM參數尋優后建立的模型可以有效提高入侵檢測的性能指標。
參考文獻
[1] ANDERSON J P. Computer sercurity threat monitoring and surveillance[R]. James PAnderson Co, Fort Washington, Pennsylvania, Aprial 1980.
[2] MUKKAMALA S, JANOSKIG I, SUNGA H. Intrusion detection using neural networks and support vector machines[C]. Proc of IEEE International Joint Conference on Neural Networks. Washington DC:IEEE Computer Society, 2002: 1702-1707.
[3] 陳光英,張千里,李星. 特征選擇和SVM訓練模型的聯合優化[J]. 清華大學學報(自然科學版),2004,44(1);9-12.
[4] SHI Y, EBERHART R. A modified particle swarm optimizer[C]. IEEE World Congress on Computational Intelligence. Piscataway:IEEE Press,1998:69-73.
[5] 龍文,梁昔明,肖金紅,等.一種動態分級的混合粒子群優化算法[J].控制與決策.2009,24(6):1406-1411.
[6] CLERC M, KENNEDY J. The particle swarm: explosion, stability, and convergence in multi-dimension complex space[J]. IEEE Transactions on Evolutionary Computation, 2002,16(1):58-73.

