1 引言
作為第四代新型節能光源的典型代表,LED 具有壽命長、節能、環保、顯色性好等其他光源無法比擬的優點, 而且隨著大功率LED 的迅速發展,越來越廣泛的應用于各種指示、顯示、背光源、普通照明和城市夜景等眾多領域。但是LED 光源發出的光不均勻,因此在對光照有嚴格要求的特殊場合的照明中,必須根據LED 本身的發光特性和預期的光強分布,來設計一個二次配光結構,將LED 的光強進行重新分配。
配光結構一般有反射面、透鏡兩種,目前LED的二次配光結構大部分采用的是透鏡結構。考慮到透鏡有兩個透光面和一定的厚度,對于任意一個曲面,若曲面設計或制作過程中稍有偏差,或透鏡中夾有一點雜質,對光線的折射和能量分布會產生很大的影響,且在實際應用中透鏡對光線有較高的吸收率而造成能量損失。而用反射面作為二次配光結構,理論上只需要一個反射面即可,容易加工且能量損失少,較好地解決了LED 均勻照明的問題。本文旨在設計一種反射面來對LED 進行二次配光。
傳統的反射面配光結構依賴于有解析解的二次曲面或二次曲面的組合。但對于發光不均勻的光源,簡單的二次曲面或二次曲面的組合都不能實現特定的光強分布。本文采用自由曲面設計的方法,根據光源的發光特性和預期的光強分布建立一個微分方程,用數值求解法求解出這個方程,根據求解結果擬合出自由反射曲面,再利用光學軟件對結果進行模擬。
2 反射面設計
本文中光源發出的光線一部分直接照射到照明面上,另一部分經設計的反射面反射到照明面上,最終在照明面上實現一個矩形的均勻照明區域。利用光的反射定律得到出射光線與入射光線的矢量的關系,再利用能量守恒和照度公式求出反射光線攜帶的能量,最后列出微分方程,通過求解微分方程得出確定自由曲面的一系列點,最終確定所需的自由曲面。
如圖1 所示,o′為光源所在的位置,建立坐標系x′o′y′。1 為照明面,為了使計算更加方便,設光源o′到照明面1 的距離為單位長度1,以o′為圓心,作一個單位球,則單位球與平面1 相切于o 點。平面2 為單位球的平行于平面1 的一個切平面。在平面1 和平面2 內分別作平行于x′,y′的x,y 軸和u,v 軸。z′軸的原點在o′處。
任一條光線與單位球面相交于p 點,則op 為單位矢量,記為i。連接o 與p 點并延長交平面2 于( u,v,1) 點,設p 點坐標為( x′,y′,z′) ,則i =( x′,y′,z′)。
如圖所示,可知x′ / u = y′ / v = ( z′ + 1) /2,且x′2 + y′2 + z′2 = 1,可求得: i = (1 + ω2 /4) ( u,v,1 - ω2 /4) ,其中ω2= u2 + v2。
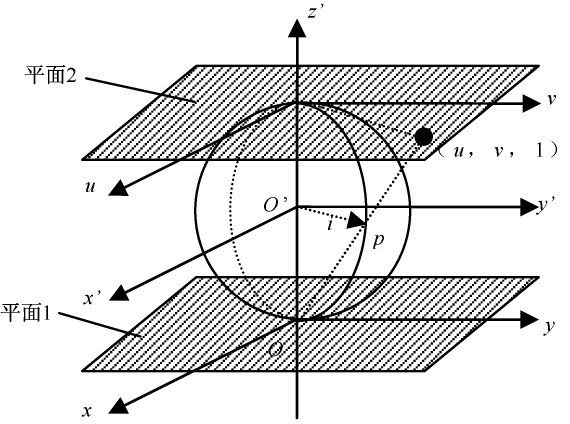
圖1 建立的坐標系
2. 1 光的反射定律
如圖2 所示,I 為LED 發出的光線,入射到到反射面上的q 點,R 為反射光線,反射到照明面上的t 點,T 為o′到t 的矢量,N 為反射面上q 點處的法線。
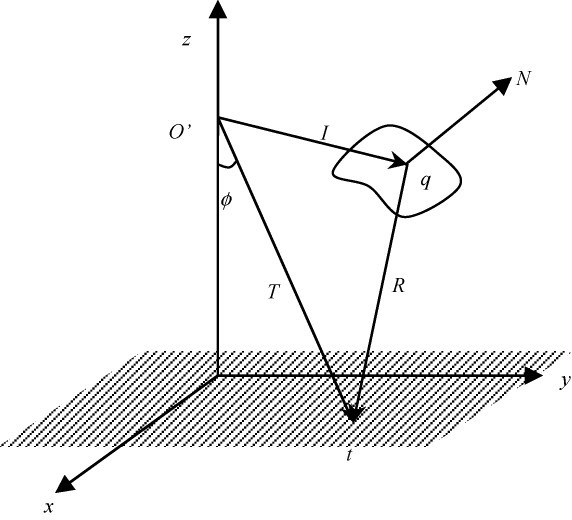
圖2 照射到t 點的反射光線光路圖
根據非成像光學理論中的反射定律:
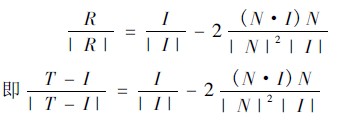
其中I = ρi,可求出矢量T 的表達式T = T ( ρ,u,v)。
由幾何關系可知反射面的法向向量為切平面內兩個矢量的矢乘,即N = Au × Av = ( ρi)u × ( ρi)v 。
由i 矢量可求出:
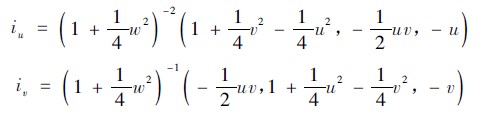
將以上三式帶入反射定律,并定義p = ρu,q =ρv,可求得T = T ( u,v,ρ,p,q) ,則反射光線反射到照明面上的點的坐標為:
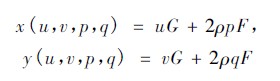
其中:
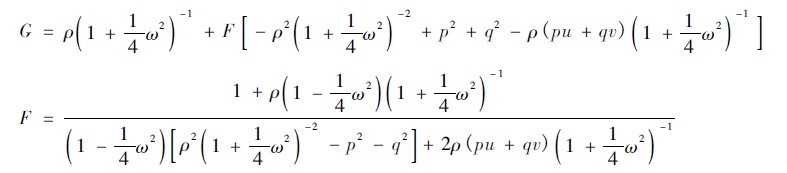
2. 2 能量守恒
LED 照明面垂直于z 軸朝下,本文采用朗伯體LED 光源,發出的光一部分直接照到照明面上,另一部分被反射后照射到照明面上,在照明面上產生一個長和寬分別為a 和b 的矩形均勻照明區域。根據能量守恒,光源的輻射通量應等于照明面上的輻射通量。
光源輻射到照明面上的輻射通量為Φ1 =∫I0 cosΦdΩ1 + ∫μI0 cosΦdΩ2,式中第一項為直接照射到照明面上的輻射通量,Ω1為該部分入射光線對應的立體角,第二項為經過反射面反射到照明面上的輻射通量,Ω2為該部分入射光線對應的立體角,μ 為反射面的反射系數。照明面上接收到的輻射通量為Φ2 = ∫ EdS,E 為照明面上的平均照度,根據能量守恒有Φ1 = Φ2。由于反射面的反射率可以高達95%以上,這里為了簡單起見,不考慮反射能量損失,且郎伯型光源的發光角度為120 度, 則![]() ,有Φ1 = Φ2,所以E = πI0 /4ab。
,有Φ1 = Φ2,所以E = πI0 /4ab。
照到t 點的光有兩束, 一束為圖示的T 光線,另一束為圖示的I 光線的反射光線,則有E = E1 +E2,其中E1為T 光束在t 點產生的照度,E2為B光束產生的照度。
如圖3 所示,設點光源的發光強度為I,被照射面積元dS′對它所張的立體角為dΩ,則照射在dS′上的光通量為dΦ′ = IdΩ = IdS′cosθ′,從而照度為E![]() 由此可求出直接照射在照明面上的光束T 在t點的照度為:
由此可求出直接照射在照明面上的光束T 在t點的照度為:
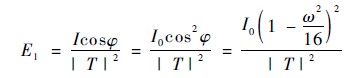
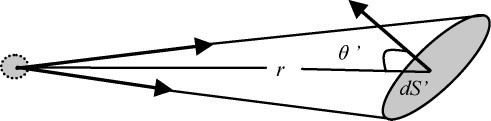
圖3 光源的照度
可求出反射到照明面上的光束R 的照度為:
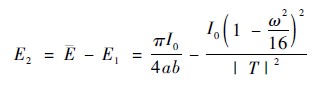
2. 3 偏微分方程
該反射過程中,入射光I 的強度I 與反射光R照到t 點的照度E2滿足偏微分方程:
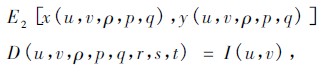
其中:
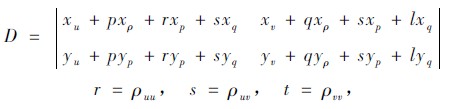
x 和y 由2. 1 中的結果給出。入射到反射面上的光線I 的強度:
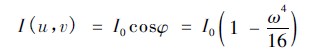
E2由2. 2 中的結果給出。將以上結果帶入偏微分方程,列出偏微分方程的具體形式。
偏微分方程的邊界條件由朗伯型光源的發光特性和矩形均勻照明區域決定。首先設置反射面的下邊緣也為一個長寬比例為a∶ b 的矩形,讓直接照射到照明面上的光為一個矩形光斑。而朗伯型LED 光源的發光角度為120°,因此反射面的上邊緣在一個頂角為120°的圓錐面上。用數值求解法將上式進行離散化,計算偏微分方程。設置反射面的下邊緣初始點坐標作為初始點條件,結合邊界條件,帶入計算機程序迭代計算方程,求出反射面上一系列的點的坐標。
3 模擬與仿真
將求解出的反射面的一系列點輸入建模軟件ProE 中,擬合成一個實體反射面,如圖4 所示。再將該反射面導入光學仿真軟件Tracepro 中,模擬驗證最終的效果,得到照明面上的照度分布圖,如圖5 所示。在中間照明區域,光照的均勻度可達85% 以上,能實現比較理想的照明效果。因為在建模過程中,是先輸入點,形成樣條曲線,再由樣條曲線形成最終的反射面,這個過程中采用了平滑的算法,引入了誤差,使最后結果有點失真,但失真程度不大。

圖4 反射面結構圖
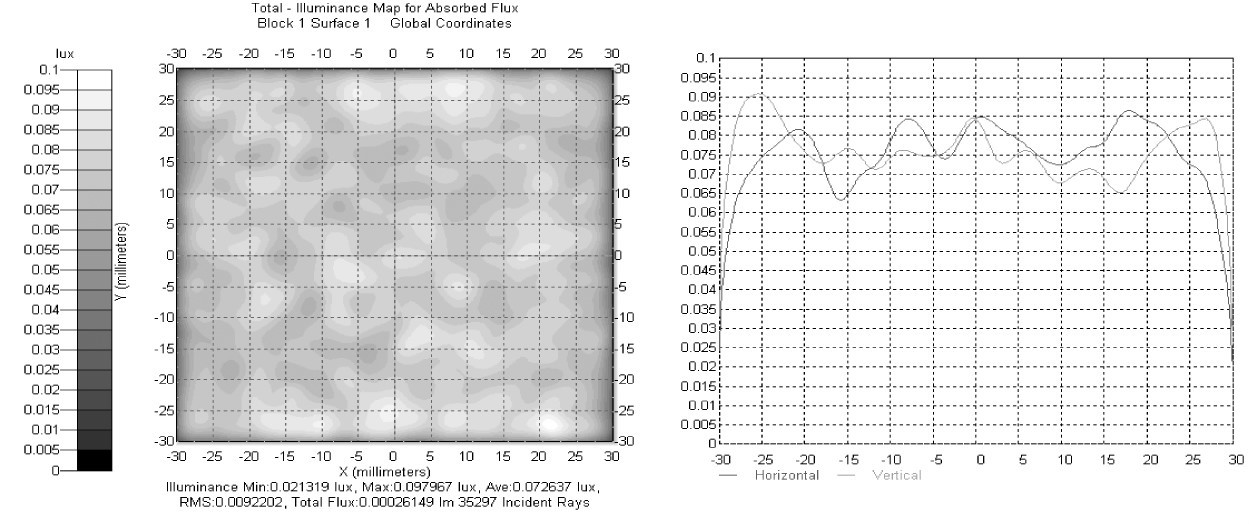
圖5 照度分布圖
4 結論
本文通過對微分方程的數值求解求出自由反射曲面的面型,依據不同的光源和照明需求得到不同的邊界條件和具體的方程,可自由設計反射曲面。
反射面型的配光結構可避免透鏡的加工成本高及對能量吸收率高等缺點。

