摘 要: 從測量矩陣和稀疏矩陣的互相關性角度出發,通過對測量矩陣和稀疏矩陣所構成的Gram矩陣進行門限選擇,進而經過相應的縮放處理降低互相關性,這樣不僅可以獲取更多有信息量的測量值,而且可以完成對測量矩陣的優化改進。通過在DWT、DCT下的壓縮感知圖像重構實驗驗證了該方法的可行性,恢復效果得到一定程度的提高,相比于傳統的小波恢復重構,達到了預期的效果。
關鍵詞: 壓縮感知;稀疏表示;測量矩陣
傳統理論指導下的信號處理首先遵循奈奎斯特/香農采樣定理對信號進行采樣,再對采樣數據進行某種變化(如DCT或DWT),將變化后幅值較大的系數進行壓縮編碼,舍棄幅值為零或接近零的系數,然后將編碼值進行存儲或傳輸,最后在解碼端通過相應的解壓縮算法恢復出原始數據。面對科技發展提出的更高要求,科學家們就構想,既然變化后的數據有些是被丟棄的,為什么還要對它進行采樣呢?是否可以直接采集那些需要的信息?針對這些問題,近年來,由DONOHO D、CANDES E和TAO T等人提出了壓縮感知理論[1-2],該理論指出,如果信號是可稀疏表示或可壓縮的,就可以通過遠少于奈奎斯特采樣率要求下數目的采樣值高概率地恢復出原始信號。本文在對矩陣的互相關性問題研究分析的基礎上進行了優化改進,并通過實驗模擬進行了有效的驗證。
1 壓縮感知的基本理論
壓縮感知發展于信息論,由于其具有高度信息挖掘的能力,在學術界和工程應用領域受到了極大關注并表現出了強大的生命力。壓縮感知是一個將采樣和壓縮合二為一的理論,即在對數據采樣的同時完成了適當的壓縮工作,該理論主要包括信號的稀疏表示、測量編碼和恢復重構。



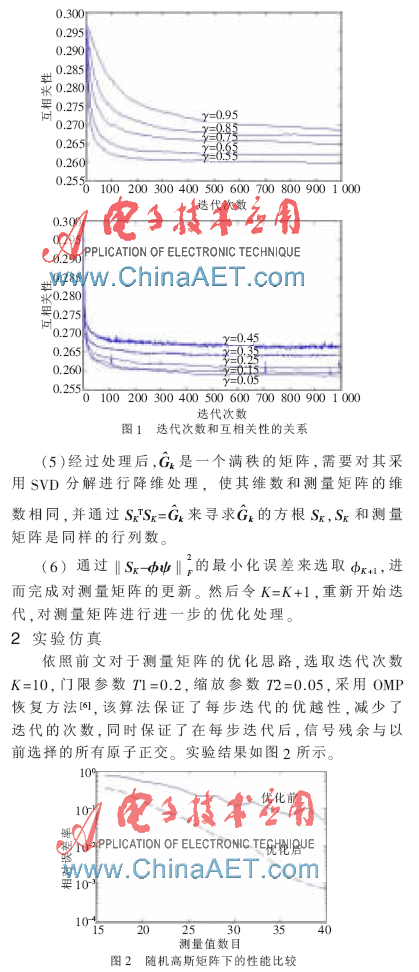
圖2中的每個點顯示了基于多次實驗的平均性能,如期望的一樣,隨著測量值數目的增加,恢復算法的性能效果得到了提升改善,在某些測量點甚至有較大幅度的提高,從而驗證了改進算法的可行性。下面就一維、二維信號進行具體的實驗分析。
針對一維信號,對測量矩陣做了相應的優化改進工作,實驗結果如圖3所示。

通過對二維圖像的恢復可以看出,以峰值信噪比(PSNR)為考量依據,經過優化后的測量矩陣對于原始的恢復有8%左右的性能提高。通過對一維、二維問題的實驗可以得出:本文所述的對測量矩陣的優化方法是可行的,針對不同的信號和問題,參數的選擇會有些差別。同樣將該理論應用于壓縮感知的離散余弦變化(DCT)問題中,恢復效果如圖5所示。

從表1可以看出,改進后的結果比改進前的結果有了一定的提高,隨著測量值數目和迭代次數的增加,都取得了一定的改進。
本文主要闡述了壓縮感知的理論框架,通過實驗仿真說明了壓縮感知能夠突破傳統采樣定理的極限,能以更少的數據采樣點高概率地恢復原始信號,并通過對測量矩陣的優化改進提高了恢復效果。實驗中假設信號的稀疏度是已知的,如何處理未知稀疏度的信號也將是今后工作研究的重點。壓縮感知作為一門新生的理論,目前還有很多問題并未解決,但是隨著研究的深入,該理論將有更廣泛的應用前景。
參考文獻
[1] DONOHO D L. Compressed sensing[C]. IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[2] CANDES E, WAKIN M. An introduction to compressive sampling[C]. IEEE Signal Processing Magazine,2008:21-30.
[3] CANDES E, ROMBERG J, TAO T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[C]. IEEE Transactions on Information Theory,2006,52(2):489-509.
[4] CANDES E J, TAO T. Near optimal signal recovery from random projections: universal encoding strategies[C]. IEEE Transactions on Information Theory, 2006,52(12):5406-5425.
[5] ELAD M. Optimized projections for compressed sensing[C]. IEEE Transactions on Signal Processing, 2007,55(12):5695-5702.
[6] TROPP J, GILBERT A. Signal recovery from random measurements via orthogonal matching pursuit[C]. Transactions on Information Theory, 2007,53(12):4655-4666.

