摘 要: 針對陀螺儀采集到的速度信號噪聲大、平滑性不好以及采用一般工程數字濾波方法對數據處理求角加速度效果不佳的問題,提出了采用Savitzky-golay濾波方法對陀螺儀采集的速度信號進行數字濾波。所得濾波結果經微分處理,得到了角加速度波形,該波形較為平滑,保留了信號的主要特征,表明了此方法的有效性。
關鍵詞: Savitzky-golay濾波;數字濾波;角加速度;微分
近年來,陀螺儀作為高精度伺服控制系統的反饋元件,用來反饋測量物體轉動的角速度。但當控制系統進行高精度控制時,就需要測量反饋角加速度的數據值。目前,角加速度的測量方法有直接法和間接法兩種[1]。為了系統不增加傳感器,提高系統的可靠性,本文采用間接法,也就是利用系統原有的速率陀螺儀進行現場采樣,采樣得到的數字角速度信號數據再進行分析與微分處理來求得角加速度值。因此,對陀螺儀采集的速度數據處理是在實際工程系統設計應用中的一個重要的環節[2-3]。
然而,在震動環境下工作的陀螺儀所采集到的數據中干擾信號量比較大,微分運算對干擾量的放大嚴重影響了求解角加速度的準確性。所以陀螺儀采集到的數據必須要經過濾波處理才能微分求解。當精度要求不高時,系統可應用輸出量為模擬信號的陀螺儀,輸出的信號可以直接經過電容等硬件濾波的方法進行平滑處理。然而,隨著控制精度的提高,系統應用于高精度的數字陀螺儀,尤其是光纖陀螺儀時,所輸出的數字信號就無法硬件濾波,必須進行軟件數字濾波的處理。目前,通常采用一般軟件數字濾波方法,如算數平均濾波、限幅濾波、中值濾波和一階滯后濾波對其測量數據進行處理,但濾波效果不是很理想。通過對多種濾波的實際計算結果進行了對比研究,提出了一種應用Savitzky-golay數值濾波來消除這些干擾信號的軟件數子濾波方法,很好地解決了這個問題。
1 一般數字濾波數據處理的局限性
1.1 陀螺儀速度信號的采集與加速度的計算
對于實時性要求很高的伺服運動控制系統來說,需要每0.002 1 s采集一個速度信號值,來達到精確的位置控制,滿足高精度的要求。然而,根據所采集到的速度信號求其所對應時刻的加速度值時,通常使用的是數值微分公式對實際測量到的原始速度數據進行數據處理。常用的數值微分公式有兩點數值微分公式和三點數值微分公式。由于三點數值微分公式相對誤差值小,因此使用三點數值微分公式對原始采樣數據進行處理,以得到相應的加速度信號[4]。
1.2 一般數字濾波數據處理的局限性
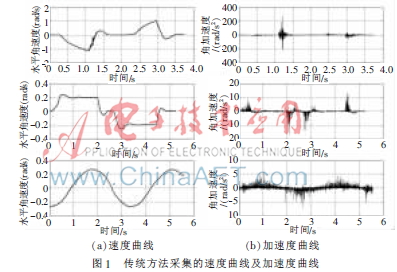
在一般數據處理中,通過陀螺儀采樣得到速度信號的原始數據,通過三點數值微分公式計算得到相應的加速度值,結果如圖1所示。
從圖1可以看出,用原始數據直接計算得到實時的加速度曲線出現了非常多的毛刺和跳躍。這是因為陀螺儀是在振動的環境下進行速度數據采集的。這些振動是難以避免的,這使得測量的數據偏移了實際數值。眾所周知,加速度是速度的一階導數,在采樣時間周期為0.002 1 s這樣非常小的數值時,對于速度的一個很小的擾動,都會對數據處理后的加速度數據產生很大的影響。從圖1(b)就可以看出,不經過濾波處理計算得到的加速度曲線毛刺和跳躍很大,沒有數據分析的價值。
目前在工程中,一般數字濾波方法主要有算數平均濾波、限幅濾波、中值濾波和一階滯后濾波。分別運用這四種方法,首先對陀螺儀采集到的速度信號進行濾波,再應用三點數值微分公式進行加速度計算。正弦速度運動應用四種不同濾波方法得到的加速度波形如圖2所示。其中,圖2(a)為5點求取平均值方法的算數平均濾波后求得的角加速度波形圖,圖2(b)為最大偏差值為0.02方法的限幅濾波后求得的角加速度波形圖,圖2(c)為連續采樣5次方法的中值濾波后求得的角加速度波形圖,圖2(d)為濾波參數a=0.2方法的一階滯后濾波后求得的角加速度波形圖。
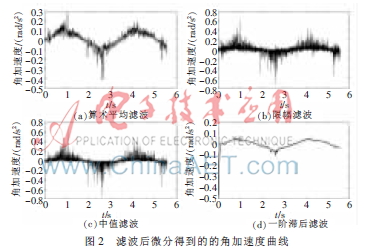
從圖2可以看出,算數平均濾波的方法較原始數據所求得角加速度的曲線圖有所平滑,但是角加速度曲線的跳躍仍然很大,取得的效果不理想,而且降低了精度;限幅濾波的方法與中值濾波的方法應用效果不明顯,毛刺以及跳躍均很大,數據分析價值不大;一階滯后濾波的方法,雖然使角加速度的波形有所平滑,但由于濾波本身方法的限制,產生了相位的滯后,與系統其他數據時域相結合分析時造成了困難,不利于進一步的數據分析。
綜上所述,由于一般數字濾波數據處理中存在局限性,不能滿足陀螺儀采集數據處理的要求。
2 基于Savitzky-golay濾波的數字濾波方法的設計實現
2.1 Savitzky-golay濾波原理[5-6]
SG濾波算法的主要思想是:通過取采集數據點xi附近固定個數的點擬合一個多項式,多項式在xi的值就給出了它的光滑數值gi(gi∈G所求光滑數值矩陣)[7]。
以nl表示xi左邊點的個數;以nr表示xi右邊的點的個數;pi(x)表示相對于點xi的一個M次多項式,用它在最小二乘意義下擬合這nl+nr+1個點。因此:
![81`BOH5FN0157K~FBB]SU65.jpg 81`BOH5FN0157K~FBB]SU65.jpg](http://files.chinaaet.com/images/2015/05/21/6356783361624073127053282.jpg)
利用這些定義,就可以用矩陣形式進行表述此問題:
min‖AB-Y‖2(4)
為求解B,使得式(4)達到最優,令AB=Y,左乘AT方程變為:
ATAB=ATY(5)
根據式(5),則可以進一步求得:
B=(ATA)-1ATY(6)
因此,可得到矩陣Y=A(ATA)-1ATY,則所求得光滑數值為
G=A(ATA)-1AT(7)
2.2 基于Savitzky-golay濾波的數字濾波方法的實現
通過濾波原理,可得出nl和nr越大,曲線的平滑性越好,不過這是以犧牲曲線特性為代價的;相反,M的取值越大,曲線特性失真率越低,但使得數據低頻部分的平滑度降低,計算量也變大[8]。
本文通過對多組實測數據進行多個不同濾波參數處理后的綜合比較,在滿足確定失真率不大的情況下,盡可能地增加平滑性,最后選擇出了所采用nl=nr=15、M=3的濾波參數。應用此參數,對陀螺儀采集的速度信號進行濾波,經過濾波后的波形以及濾波后求得的角加速度的波形圖如圖3所示。
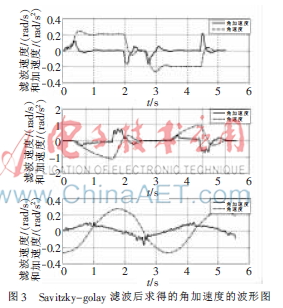
下面選擇采取SSE(誤差平方和)和RMSE(標準差)的技術指標來評價在正弦速度運動的采集信號經不同種濾波方法處理后的濾波效果,如表1所示。
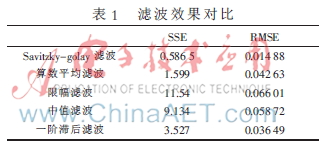
從圖3、表1可以看出,原始數據經過Savitzky-golay濾波后數據得到了平滑,SSE值和RMSE值也越接近于0,有效地消除了毛刺,較好地保證了經過濾波后速度信號數據,并且依舊保留了信號的主要特征,消除了干擾信號。這樣,對濾波后的速度信號再進行數據微分處理,得到的加速度曲線基本上消除了毛刺以及各種跳躍,而且沒有時間滯后現象的發生,有利于對數據進行進一步處理,進而為設計高精度的控制系統提供了依據。
本文針對陀螺儀采集到的速度數據信號進行微分處理中遇到的問題,進行了采用不同濾波方法的分析與研究。提出了將Savitzky-golay濾波方法應用到此數據處理中,發現Savitzky-golay濾波方法在進行陀螺儀速度信號處理方面取得了較好的效果,而且此濾波方法是一種不受原始數據本身限制的低通平滑濾波算法,并不需計算濾波的截止頻率。最后通過實際計算得到的濾波后的速度波形和加速度波形可以看出,Savitzsky-golay濾波方法較工程上的傳統濾波方法在去噪效果和數據微分方面有了一定程度的改進。
參考文獻
[1] OVASKA S J, VALIVIITA S. Angular acceleration measurement: a review[J]. IEEE Transactions on Instrumenta-tion and Measurement, 1998,47(5):1211-1217.
[2] 卓斌.速度陀螺儀采樣數據的分析研究[J].計算機測量與控制,2006,14(9):1213-1215.
[3] ROMMANEE J, PIOTR P, VANJA G, et al. A method for dead reckoning parameter correction in pedestrian navigation system[J]. IEEE Transactions on Instrumentation and Measure-ment, 2003,52(1):209-215.
[4] 李廣華,張愛民,張杭,等.Savitzky-golay濾子在斷路器在線檢測數據處理中的應用[J].高壓電器,2005,41(3):225-227.
[5] 蔡天凈,唐瀚.Savitzky-Golay平滑濾波器的最小二乘擬合原理綜述[J].數字通訊,2011,01(017):63-68.
[6] GANDER W, HREBIEEK J, BARTON S. Solving Problem in Scientific Computing Using Maple and Matlab[M]. Berlin: Springer-verlag, 1993.
[7] 桑慶雙,程健.SG濾波在朗繆爾探針信號處理中的應用[J].計算機工程,2011,37(17):220-226.
[8] PRICHARD D, THEILER J. Generating surrogate data for time series with several simultaneously measured variables[J]. PhysicalReview Letters, 1994, 73(7): 951-954.

