0 引言

    世界上每年因戰爭、自然災害、交通事故等原因引起的殘疾人數多達千萬人以上，其中大部分為肢體殘疾，而目前市場上的大部分假肢都是作為裝飾性用品，真正實現功能代償的假肢數量較少。為滿足殘疾人日常生活的需求，本系統對前臂假肢做了姿態規劃，即控制前臂旋轉和手腕俯仰兩個電機，使得假肢末端手爪的虎口平面與大地水平面始終保持平行，如圖1所示。這樣假肢在抓取和移動目標物體的過程中，可以保證運動平穩，對移動水杯等類似操作尤其重要。在前臂假肢的平衡控制過程中，姿態傳感器將檢測到的前臂假肢的姿態信號送入STM32，經算法運算得到控制量驅動舵機來控制前臂的扭轉和手部的俯仰，從而使前臂假肢的手部恢復到平衡狀態。可以看出，獲取實時的前臂假肢的姿態是保持手部平衡的前提。因此，實現一種實時可靠的前臂假肢姿態估計算法尤為重要，它直接影響其手部自平衡性能。

    姿態解算的算法有多種，常用的算法有歐拉角法、方向余弦法與四元數法，由于歐拉角法求解時，方程中存在奇點，方向余弦法計算量大，因此現在常用的方法為四元數法，其計算量小，無奇點^[1-2]。姿態估計算法必須考慮到傳感器容易受溫度及噪聲的影響而產生不同程度的漂移，它會影響姿態估計的準確性。針對這一問題，本文采用卡爾曼濾波的方法來融合陀螺儀和加速度計輸出的數據，修正了陀螺儀輸出量中的隨機漂移分量^[3]。

1 系統硬件設計

    隨著安卓智能手機的發展與普及，為了讓前臂假肢的控制更加方便和標準化，提出了以安卓手機離線識別語音及應用藍牙通信技術實現安卓手機無線控制假肢運動的方案。本文介紹的前臂假肢可實現手部平衡，除此之外，在不需要手部保持平衡的環境下，安卓手機通過語音識別可控制前臂假肢關閉手部自平衡功能和實現手部上抬、下落、內轉、外轉和張合等動作。該系統由安卓手機、藍牙模塊、MPU6050、STM32微控制器、MX-28高性能舵機組成，系統的控制流程如圖2所示。

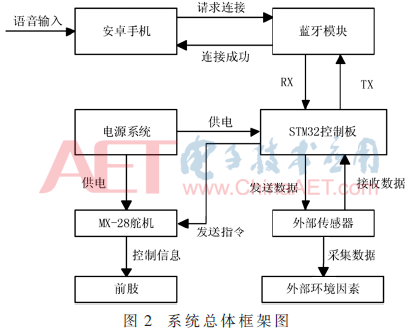
    其中，選用MPU6050做為前臂假肢的姿態檢測系統，MPU6050在單個產品封裝內集成了3軸陀螺儀和3軸加速度計。由于前臂假肢不需獲知偏航角，所以本文采用了MPU6050來獲取前臂假肢的俯仰角和橫滾角。整個控制過程由MPU6050測量姿態變化，并通過前臂扭轉以及手腕俯仰來根據姿態變化實時進行調整，使其達到自平衡狀態。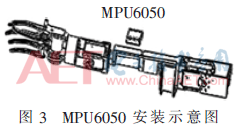

    MPU6050安裝在假肢的腕部，其安裝位置如圖3所示。將MPU6050安裝在控制前臂旋轉關節的上部并固定在連桿上，左右位置可以變化，但要確保其所在的平面與手爪虎口所在平面平行。安裝完成后，前臂繞MPU6050的X軸旋轉，手腕繞MPU6050的Y軸俯仰。

2 四元數姿態解算算法

    四元數的數學概念是1843年由哈密頓首先提出的。它是由一個實部單位和3個虛部單位i、j、k組成，其形式為：q=q₀+q₁i+q₂j+q₃k。四元數可以表示旋轉，其標量部分表示旋轉角度的大小，矢量部分表示轉軸的方向^[4-5]，應用四元數時必須進行歸一化，也就是令其模值為1。

    前臂假肢的定位由固定的內部的三維坐標確定，一個坐標系到另一個坐標系的變換，可以通過繞不同坐標軸的3次連續轉動來實現。順時針繞橫滾軸，即繞載體坐標系的X軸旋轉，得到橫滾角φ；順時針繞俯仰軸，即繞載體坐標系的Y軸旋轉，得到俯仰角θ；順時針繞偏航軸，即繞載體坐標系的?爪軸旋轉，得到偏航角γ^[6]。

    四個參數的初始值是由歐拉角的初始值經過以下計算得到的^[6-9]：

    利用四元數微分方程可以實現四元數的更新，其中，ω是陀螺儀測量的角速度。

    應用四階龍格—庫塔算法解微分方程，得到4個參數的更新值。具體過程如下^[12-14]：

    設：

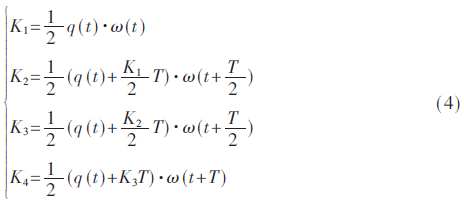
    則：

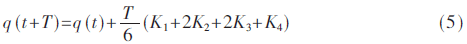
其中，T為更新周期，q(t)為初始四元數，q(t+T)為更新后的四元數，K₁是時間段T開始時的斜率，K₂是時間段中點的斜率，K₃也是中點的斜率，K₄是時間段終點的斜率。

    計算得到這4個參數之后，可由姿態矩陣T更新歐拉角[15]：

    得到姿態角，即可得到前臂假肢的姿態估計。

    前臂假肢在平衡的情況下，歐拉角的理想輸出值應該是0°，但由于陀螺儀有隨機漂移誤差，歐拉角會一直積累^[16]。實驗結果圖4所示。

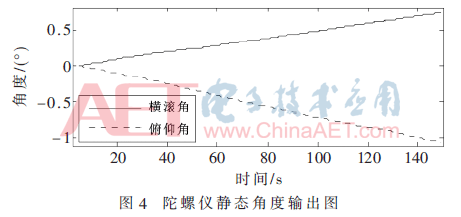
    針對這一問題，提出了應用卡爾曼濾波的數據融合算法來解決。卡爾曼濾波可以將陀螺儀的輸出數據和加速度計的輸出數據融合起來。陀螺儀用于測量角速度，動態跟蹤性能好，但陀螺儀受溫度、不穩定力矩等因素的影響，會產生隨機漂移誤差；加速度計可用于測量加速度，通過測得的加速度值與重力加速度的比值得到傾角值，加速度計靜態性能好，但是動態跟蹤性能差。可以看出，陀螺儀和加速度計優缺點互補，結合起來會有好的效果^[17-18]。

3 實驗結果分析

3.1 四元數法和卡爾曼濾波實驗結果分析

    將MPU6050靜止平放在桌上，采集其經四元數姿態解算和卡爾曼濾波后輸出的數據，通過MATLAB工具對實測數據進行仿真分析，如圖5所示，俯仰角和橫滾角都在附近，對比圖4發現卡爾曼濾波有效解決了陀螺儀的隨機漂移誤差，可以準確地獲取靜態時前臂假肢的姿態。

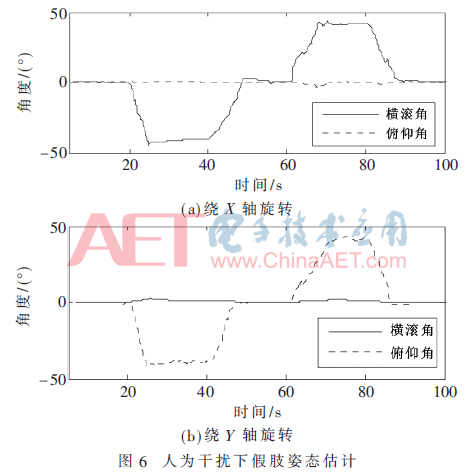
    將MPU6050安裝到前臂假肢上，令前臂假肢繞MPU6050的X軸從平衡位置順時針逐步旋轉到-40°，一段時間后，回到平衡位置，再沿X軸逆時針逐步旋轉到40°，采集這一過程MPU6050經四元數姿態解算和卡爾曼濾波后輸出的數據，通過MATLAB工具對實測數據進行仿真分析，橫滾角發生相應的變化，俯仰角基本保持不變，如圖6(a)所示。令前臂假肢繞MPU6050的Y軸重復以上實驗，根據圖6(b)可以看出，俯仰角發生相應的變化，橫滾角基本保持不變。由于實驗過程中手動旋轉前臂假肢，操作者偶有抖動和難做到勻速轉動，因此，圖6中的波形中偶有小的波動。實驗表明，本文采用的姿態估計可以實現前臂假肢動作時姿態的正確估計，經過STM32運算處理后，實現前臂假肢在運動過程中保持手部平衡。

3.2 前臂假肢手部自平衡實驗結果分析

    對前臂假肢系統組裝并調試，通過安卓手機軟件向假肢發出保持手部平衡的命令。具體測試步驟:連接好線路，打開電源，觀察指示燈正常亮起，觸擊控制界面的藍牙連接按鈕，觀察指示燈，以確保手機藍牙和藍牙模塊的配對連接成功；否則，檢查系統的連接是否正確。藍牙配對成功后，向安卓手機喊出“平衡”指令，手機通過藍牙將指令傳到單片機，從而控制前臂假肢運動。實驗結果如圖7、圖8所示。

    圖7(a)～圖7(e)展示了前臂假肢從下往上轉動過程中，其手部可以實現自平衡，手部虎口一直保持與大地平行。

    圖8中以箭頭指向的地點為參考點，可以看出圖8(a)～圖8(c)為前臂假肢由內往外轉動過程，同樣假肢手部能實現自平衡。

4 結論

    此前臂假肢采用四元數法的姿態解算算法，并利用卡爾曼濾波融合MPU6050中陀螺儀和加速度計的數據，得到其正確的姿態估計。經實驗測試，該系統運行穩定、可靠，所設計的姿態估計算法能夠很好地跟蹤前臂假肢的真實姿態，實現了假肢手部的姿態自平衡控制。此前臂假肢可以輔助殘疾人完成喝水等動作，方便了他們的生活，也減輕了家屬的負擔。

參考文獻

[1] 杜海龍，張榮輝，劉平，等.捷聯慣導系統姿態解算模塊的實現[J].光學精密工程，2008，16(10)：1956-1962.

[2] 張榮輝，賈宏光，陳濤，等.基于四元數法的捷聯式慣性導航系統的姿態解算[J].光學精密工程，2008，16(10)：1963-1970.

[3] 楊凌霄，李曉陽.基于卡爾曼濾波的兩輪自平衡車姿態解算方法[J].計算機仿真，2014，31(6)：406-409.

[4] 葉锃鋒，馮恩信.基于四元數和卡爾曼濾波的兩輪車姿態穩定方法[J].傳感技術學報，2012，25(4)：524-528.

[5] 呂印新，肖前貴，胡壽松.基于四元數互補濾波的無人機姿態解算[J].燕山大學學報，2014,38（2）：175-180.

[6] 張思奇，趙憶文.便攜式移動機器人姿態解算方法[J].微計算機信息，2007，23(10-2)：188-190.

[7] 祝喬，汪旭東，崔家瑞.基于四元數的航天器姿態非線性控制器[J].信息與控制，2012，41(2)：170-179.

[8] 賈秋玲，閆建國，王建民.空間多剛體系統姿態的協同控制[J].信息與控制，2005，34(4)：385-388.

[9] 趙國文.機器人運動學中的四元數矩陣和基變換矩陣[J].機器人，1993，15（2）：59-64.

[10] 張天光，王秀萍，王麗霞，等，譯.捷聯慣性導航技術(第二版)[M].北京：國防工業出版社，2007：29-33.

[11] 秦永元.慣性導航[M].北京：科學出版社，2006：287-305.

[12] 崔璐璐.基于MEMS器件的姿態測量系統研究與實現[D].大連：大連理工大學，2009.

[13] 王勵揚，霍昆明，何文濤，等.四階龍格庫塔算法在捷聯慣性導航中的應用[J].計算機仿真，2014，31(11)：56-59.

[14] 張慧春，吳簡彤，何昆鵬，等.四階龍格-庫塔法在捷聯慣導系統姿態解算中的應用[J].應用科技，2005，32(6)：37-39.

[15] 鄧正隆.慣性技術[M].哈爾濱：哈爾濱工業大學出版社，2006：14-164.

[16] 金光明，張國良，陳林鵬.MEMS陀螺儀靜態漂移模型與濾波方法研究[J].傳感器與微系統，2007，26(11)：48-50.

[17] 馮智勇，曾瀚，張力，等.基于陀螺儀及加速度計信號融合的姿態角度測量[J].西南師范大學學報(自然科學版)，2011，36(4)：137-141.

[18] 劉星.多維MEMS慣性傳感器的姿態解算算法研究[D].哈爾濱：哈爾濱工程大學，2013.